题目内容
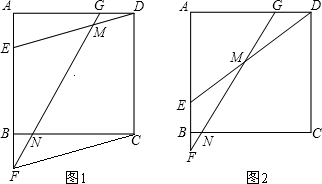
13.如图1、2,AB∥CD,直线a分别交AB、CD于点E、F,点M在EF上,P是直线CD上的一个动点,(点P不与F重合)①在图1中,若∠1=50°,∠3=30°,求∠2的度数
②在图1中,当点P在射线FC上移动时,∠2+∠3=∠1成立吗?请说明理由;
③在图2中,当点P在射线FD上移动时,∠4+∠5与∠1有什么关系?说明理由.

分析 ①根据AB∥CD,得到∠1+∠MFP=180°,根据三角形的内角和即可得到结果;
②根据平行线的性质和三角形的内角和定理即可得到结论;
③根据AB∥CD,得到180°-∠BEM=∠MFP,根据平角的定义得到180°-∠4=∠FMP,由外角的性质得到∠MFP+∠FMP=∠5,然后根据等式的性质即可得到结论.
解答 解:①∵AB∥CD,
∴∠1+∠MFP=180°,
∵∠1=50°,
∴∠MFP=130°,
∵∠3=30°
∴∠2=180°-130°-30°=20;
②成立,
理由:∵AB∥CD,
∴∠1+∠MFP=180°,
∵∠2+∠3+∠MFP=180°,
∴∠2+∠3=∠1;
③∠4+∠5-∠1=180°,
理由:∵AB∥CD,
∴∠BEM+∠MFP=180°,
∴180°-∠BEM=∠MFP,
∵180°-∠4=∠FMP,
∵∠MFP+∠FMP=∠5,
∴180°-∠BEM+180°-∠4=∠5,
∴∠BEM+∠4+∠5=360°,
∵∠BEM=180°-∠1,
∴180°-∠1+∠4+∠5=360°,
∴∠4+∠5-∠1=180°.
点评 本题考查了平行线的性质,三角形的内角和,外角的性质,熟练掌握平行线的性质定理是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
13.下列对方程2x2-7x-1=0的变形,正确的是( )
| A. | (x+$\frac{7}{4}$)2=$\frac{57}{16}$ | B. | (x-$\frac{7}{4}$)2=$\frac{57}{16}$ | C. | (x-$\frac{7}{4}$)2=$\frac{81}{16}$ | D. | (x+$\frac{7}{4}$)2=$\frac{41}{16}$ |
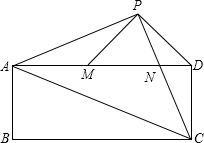 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.