题目内容
9.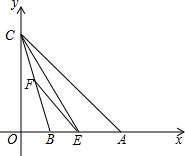 如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.
如图,在平面直角坐标系xOy中,已知点A的坐标为(6,0),点C的坐标为(0,6),tan∠CBO=$\frac{1}{3}$,E是线段AB上的一个动点(与点A、点B不重合),过点E作EF∥AC交BC于点F,连结CE.(1)求AC和OB的长;
(2)设AE的长为m,△CEF的面积为S,求S与m之间的函数关系式;
(3)在(2)的条件下试说明S是否存在最大值?若存在,请求出S的最大值,并求出此时点E的坐标.
分析 (1)先求出OA、OC的长度,结合tan∠CBO=$\frac{1}{3}$,求出AC,在Rt△OAC中利用勾股定理可得出OB.
(2)AE=m,则BE=4-m,利用△BEF∽△BAC得出${(\frac{BE}{BA})^2}=\frac{{S_{△BEF}}}{{S_{△BAC}}}$,即${(\frac{4-m}{4})^2}=\frac{{S_{△BEF}}}{{S_{△BAC}}}$,求出△BEF的面积,再由S=S△BCE-S△BFE即可得出答案;
(3)结合(2)的表达式,利用配方法求函数最值即可,算出m的值后可得出点E坐标,也可判断此时△BCE的形状.
解答 解:(1)∵点A的坐标为(6,0),点C的坐标为(0,6),
∴OA=6,OC=6,
由勾股定理得到AC=$6\sqrt{2}$,
在Rt△BOC中,tan∠CBO=$\frac{1}{3}$
∴BO=2;
(2)依题意,AE=m,则BE=4-m,
∵EF∥AC,
∴△BEF∽△BAC.
∴${(\frac{BE}{BA})^2}=\frac{{S_{△BEF}}}{{S_{△BAC}}}$,
即${(\frac{4-m}{4})^2}=\frac{{S_{△BEF}}}{{S_{△BAC}}}$,
∵S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}×4×6$=12,
∴S△BEF=$\frac{3}{4}$(4-m)2,
∴$S_{△EFC}=S_{△CBE}-S_{△BEF}=3(4-m)-\frac{3}{4}{(4-m)^2}=-\frac{3}{4}m(m-4)$,
自变量m的取值范围是0<m<4.
(3)S存在最大值.
∵$S=-\frac{3}{4}m(m-4)=-\frac{3}{4}{(m-2)^2}+3$,
∴当m=2时,S有最大值,S最大值=3,
∵AE=m=2,
∴OE=OA-AE=4,
∴点E的坐标为(4,0).
点评 本题考查了相似形综合题,涉及了三角函数、点的坐标与线段长度之间的转换,解答本题要求我们熟练掌握配方法求二次函数最值的关系,难度较大.

 阅读快车系列答案
阅读快车系列答案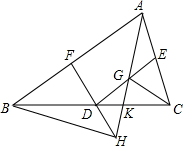 如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH.
如图,在△ABC中,D、E、F分别是三边BC、AC、AB的中点,连结DE,在DE上任取一个点G,AG的延长线交FD的延长线于H,交CD于K,连结CG.求证:CG∥BH. 如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?
如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?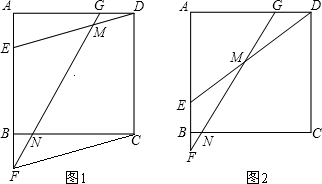
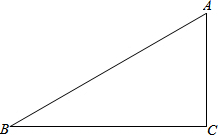 如图,在△ABC中,AB=17,BC=15,AC=8.
如图,在△ABC中,AB=17,BC=15,AC=8.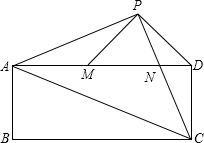 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.