题目内容
16.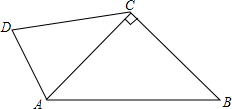 如图,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方形旋转90°得到DA′,连接BA′,则线段BA′的长度是4$\sqrt{2}$.
如图,在四边形ABCD中,AC⊥BC,且AC=BC,CD=4,若将线段DA绕点D按逆时针方形旋转90°得到DA′,连接BA′,则线段BA′的长度是4$\sqrt{2}$.
分析 首先证明△ABC和△AA′D为等腰直角三角形,从而求得AB:AC=$\sqrt{2}$,$\frac{AA′}{AD}=\frac{AB}{AC}$,然后再证明∠A′AB=∠DAC,从而可证明△CAD∽△BA′A,最后利用相似三角形的性质可求得A′B的长度.
解答 解:如图所示:
∵AC⊥BC,且AC=BC,
∴△ABC为等腰直角三角形.
∴$\frac{AB}{AC}=\sqrt{2}$.
∵将线段DA绕点D按逆时针方形旋转90°得到DA′
∴△AA′D为等腰直角三角形.
∴△ABC∽△AA′D.
∴$\frac{AA′}{AD}=\frac{AB}{AC}$.
又∵∠CAB=∠A′AD,
∴∠A′AB=∠DAC.
∵$\frac{AA′}{AD}=\frac{AB}{AC}$且$\frac{AA′}{AD}=\frac{AB}{AC}$,
∴△CAD∽△BA′A.
∴$\frac{A′B}{CD}=\frac{AB}{AC}$,即:$\frac{A′B}{4}=\sqrt{2}$.
∴A′B=4$\sqrt{2}$.
点评 本题主要考查的是旋转的性质、等腰三角形的性质、相似三角形的性质和判定,证得△CAD∽△BA′A是解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
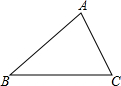 推理与证明:
推理与证明: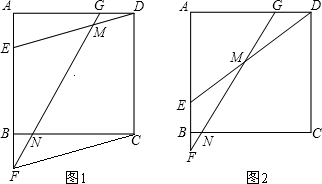
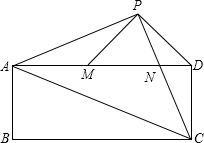 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.