题目内容
2.把下列各式因式分解:(1)-12a2b+24ab2;
(2)8a(x-y)2-4b(y-x);
(3)2(a-3)2-a+3;
(4)(a+b)2+(a+b)(a-3b);
(5)(x2+3x)-3(x+3);
(6)$\frac{1}{2}$a2(x-2a)2-$\frac{1}{4}$a(2a-x)3.
分析 (1)直接提取公因式-12ab,进而分解因式得出即可;
(2)直接提取公因式4(x-y),进而分解因式得出即可;
(3)直接提取公因式(a-3),进而分解因式得出即可;
(4)首先去括号,进而合并同类项,再利用平方差公式分解因式即可;
(5)直接利用提取公因式法分解因式得出即可;
(6)直接利用提取公因式法分解因式得出即可.
解答 解:(1)-12a2b+24ab2=-12ab(a-b);
(2)8a(x-y)2-4b(y-x)=4(x-y)[2a(x-y)+b];
(3)2(a-3)2-a+3
=(a-3)[2(a-3)-1]
=(a-3)(2a-7);
(4)(a+b)2+(a+b)(a-3b)
=a2+2ab+b2+a2-2ab-3b2
=2(a2-b2)
=2(a+b)(a-b);
(5)(x2+3x)-3(x+3)=(x+3)(x-3);
(6)$\frac{1}{2}$a2(x-2a)2-$\frac{1}{4}$a(2a-x)3
=$\frac{1}{4}$a(x-2a)2[2a+(x-2a)]
=$\frac{1}{4}$ax(x-2a)2.
点评 此题主要考查了提取公因式法以及公式法分解因式,正确找出公因式是解题关键.

练习册系列答案
相关题目
13.下列对方程2x2-7x-1=0的变形,正确的是( )
| A. | (x+$\frac{7}{4}$)2=$\frac{57}{16}$ | B. | (x-$\frac{7}{4}$)2=$\frac{57}{16}$ | C. | (x-$\frac{7}{4}$)2=$\frac{81}{16}$ | D. | (x+$\frac{7}{4}$)2=$\frac{41}{16}$ |
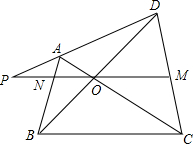 已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN.
已知:如图所示,在四边形ABCD中,对角线AC,BD相交于点O,MO∥BC,MO的延长线交AB于点N,交DA的延长线于点P.求证:PO2=PM•PN. 如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?
如图是边长为1的正方形组成的方格图,图中虚线组成的正方形的边长a是有理数还是无理数?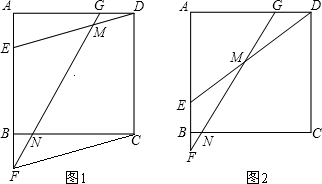
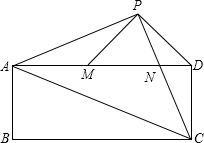 已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.
已知:如图,在矩形ABCD中,AC是对角线,点P为矩形外一点且满足AP=PC,AP⊥PC,PC交AD于点N,连接DP,过点P作PM⊥PD交AD于M.