题目内容
4.2015年秋,由于环境污染严重,我国多地出现持续雾霾,某工厂看到商机,加急研发一种专用口罩,工厂接到订单生产高、中、低档专用型口罩共2400个,厂方计划由20个工人一天内加工完成,并要求每人只加工一种类型口罩,根据下表提供的信息,解答下列问题:| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
分析 (1)由利润=生产个数×单个获利,可列出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)①根据生产口罩数=单人生产数×人数,可找出关于x、y的二元一次方程,将x当成自变量变形即可得出y与x之间的函数关系式;
②根据加工每种类型口罩的人数均不少于3人,列出关于x、y的二元一次不等式组,解不等式组即可得出x的取值范围,在此范围内取正整数即可得出结论;
③根据利润=生产个数×单个获利,找出三种方案下的获利情况,比较即可得出结论.
解答 解:(1)根据题意可知:$\left\{\begin{array}{l}{3×160a+2×120b=4800}\\{2×160a+3×120b=4800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=6}\\{b=8}\end{array}\right.$.
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,则加工低档口罩的人数为20-x-y,
根据已知得:160x+120y+100(20-x-y)=2400,
即y=-3x+20.
故y与x之间的函数关系式为y=-3x+20.
②由已知得:$\left\{\begin{array}{l}{x≥3}\\{y=-3x+20≥3}\\{20-x-y≥3}\end{array}\right.$
解得:3≤x≤$\frac{17}{3}$,
∴x=3,4,5.
∴安排方案有三种:高档3人,中档11人,低档6人;高档4人,中档8人,低档8人;高档5人,中档5人,低档10人.
③第一种方案利润:3×160×6+11×120×8+6×100×5=16440(元);
第二种方案利润:4×160×6+8×120×8+8×100×5=15520(元);
第三种方案利润:5×160×6+5×120×8+10×100×5=14600(元).
∵16440>15520>14600,
∴第一种方案利润最大,最大为16440元.
点评 本题考查了二元一次方程组得应用、解二元一次不等式组以及一次函数的应用,解题的关键是:(1)列出关于a、b的二元一次方程组;(2)①由总量找出x、y间的关系;②解二元一次不等式组;③求出三种方案的利润并比较大小.本题属于中档题,难度不大,解决该题型题目时,根据数量关系列出方程(或方程组)是关键.

| A. | -6 | B. | -5 | C. | 4 | D. | -4 |
| A. | y=-x | B. | y=$\frac{1}{x}$ | C. | y=3-2x | D. | y=x2 |
| A. | 内角和与外角和相等的多边形是四边形 | |
| B. | 十边形的内角和为1440° | |
| C. | 多边形的内角中最多有四个直角 | |
| D. | 十边形共有40条对角线 |
 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.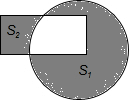 如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π)
如图,在半径为4的圆中,阴影部分图形的面积为S1;在边长为4,2的矩形中,阴影部分的面积为S2,则S1-S2的值为16π-8.(结果保留π) 如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.