题目内容
15. 如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.
如图,四边形ABCD中,∠A=∠ABC=90°,AD=10cm,BC=30cm,E是边CD的中点,连接BE并延长与AD的延长线相交于点F.(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
分析 (1)根据同旁内角互补两直线平行求出BC∥AD,再根据两直线平行,内错角相等可得∠CBE=∠DFE,然后利用“角角边”证明△BEC和△FCD全等,根据全等三角形对应边相等可得BE=EF,然后利用对角线互相平分的四边形是平行四边形证明即可;
(2)分三种情况:①BC=BD时,由勾股定理列式求出AB,由平行四边形的面积公式列式计算即可得解;
②BC=CD时,过点C作CG⊥AF于G,证出四边形AGCB是矩形,由矩形的对边相等得AG=BC=3,求出DG=2,由勾股定理列式求出CG,由平行四边形的面积列式计算即可;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=2,矛盾.
解答 (1)证明:∵∠A=∠ABC=90°,
∴BC∥AD,
∴∠CBE=∠DFE,
在△BEC与△FED中,
$\left\{\begin{array}{l}{∠CBE=∠DFE}&{\;}\\{∠BEC=∠FED}&{\;}\\{CE=DE}&{\;}\end{array}\right.$,
∴△BEC≌△FED(AAS),
∴BE=FE,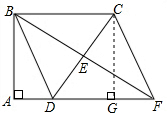
又∵E是边CD的中点,
∴CE=DE,
∴四边形BDFC是平行四边形;
(2)解:分三种情况:①BC=BD=30cm时,
由勾股定理得,AB=$\sqrt{B{D}^{2}-A{D}^{2}}$=$\sqrt{3{0}^{2}-1{0}^{2}}$=20$\sqrt{2}$(cm),
∴四边形BDFC的面积=30×20$\sqrt{2}$=600$\sqrt{2}$(cm2);
②BC=CD=30时,过点C作CG⊥AF于G,如图所示:
则四边形AGCB是矩形,
∴AG=BC=30,
∴DG=AG-AD=30-10=20,
由勾股定理得,CG=$\sqrt{C{D}^{2}-D{G}^{2}}$=$\sqrt{3{0}^{2}-2{0}^{2}}$=10$\sqrt{5}$,
∴四边形BDFC的面积=30×10$\sqrt{5}$=300$\sqrt{5}$;
③BD=CD时,BC边上的中线应该与BC垂直,从而得到BC=2AD=20,矛盾,此时不成立;
综上所述,四边形BDFC的面积是600$\sqrt{2}$cm2或300$\sqrt{5}$cm2.
点评 本题考查了平行四边形的判定与性质,等腰三角形的性质,全等三角形的判定与性质,(1)确定出全等三角形是解题的关键,(2)难点在于分情况讨论.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案| A. | 一组数据:4、1、3、1、2的中位数是3 | |
| B. | 了解一批节能灯的使用寿命,适合用普查的方式 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 甲、乙两人在相同条件下各射击20次,他们的成绩平均数相同,方差分别是S甲2=0.4.S乙2=0.6,则甲的射击成绩较稳定 |
| A. | 100° | B. | 40° | C. | 100°或40° | D. | 60° |
| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
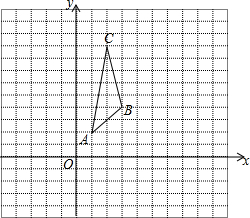 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).