题目内容
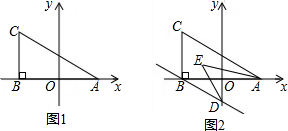
19. 如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
如图所示,在一张长为4cm、宽为3cm的矩形纸片上,现要剪下一个腰长2cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,另两个顶点在矩形的边上),则剪下的等腰三角形面积为2或$\sqrt{3}$cm2.
分析 根据题意画出符合题意的图形,进而得出答案.
解答  解:如图1,等腰三角形面积为:$\frac{1}{2}$×2×2=2,
解:如图1,等腰三角形面积为:$\frac{1}{2}$×2×2=2,
如图2,等腰三角形的高为:$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
则其面积为:$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.
故答案为:2或$\sqrt{3}$.
点评 此题主要考查了勾股定理以及等腰三角形的性质,正确画出图形是解题关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
9.-$\frac{1}{6}$的倒数的相反数是( )
| A. | $\frac{1}{6}$ | B. | 6 | C. | -$\frac{1}{6}$ | D. | -6 |
7.若等腰三角形的一个内角是40°,则它的顶角是( )
| A. | 100° | B. | 40° | C. | 100°或40° | D. | 60° |
14. 直线l1∥l2,一块含45°角的直角三角板,如图放置,∠1=42°,则∠2等于( )
直线l1∥l2,一块含45°角的直角三角板,如图放置,∠1=42°,则∠2等于( )
 直线l1∥l2,一块含45°角的直角三角板,如图放置,∠1=42°,则∠2等于( )
直线l1∥l2,一块含45°角的直角三角板,如图放置,∠1=42°,则∠2等于( )| A. | 97° | B. | 93° | C. | 87° | D. | 83° |
4.2015年秋,由于环境污染严重,我国多地出现持续雾霾,某工厂看到商机,加急研发一种专用口罩,工厂接到订单生产高、中、低档专用型口罩共2400个,厂方计划由20个工人一天内加工完成,并要求每人只加工一种类型口罩,根据下表提供的信息,解答下列问题:
(1)若工厂安排3人加工高档口罩、2人加工中档口罩和安排2人加工高档口罩、3人加工中档口罩均获利4800元,请求a、b的值;
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
| 口罩种类 | 高档 | 中档 | 低挡 |
| 每人可加工口罩的数量(个) | 160 | 120 | 100 |
| 每个口罩获利(元) | a | b | 5 |
(2)①设加工高档口罩的人数为x,加工中档口罩的人数为y,求y与x之间的函数关系式;
②如果加工每种类型口罩的人数均不少于3人,那么加工口罩的人数安排方案有几种?并写出每种安排方案;
③要使此次加工口罩的利润最大,应采用②中哪种方案?并求出最大利润.
9.水果商贩小李去水果批发市场采购被誉为“果中之王”的泰顺猕猴桃,他了解到猕猴桃有精品盒与普通盒两种包装,精品盒的批发价格每盒60元,普通盒的批发价格每盒40元,现小李购得精品盒与普通盒共60盒,费用共为3100元.
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
小李希望在甲店获利不少于1000元的前提下,使自己获取的总利润W最大,应该如何分配?最大的总利润是多少?
(1)问小李分别购买精品盒与普通盒多少盒?
(2)小李经营着甲、乙两家店铺,每家店铺每天部能售出精品盒与普通盒共30盒,并且每售出一盒精品盒与普通盒,在甲店获利分别为30元和40元,在乙店获利分别为24元和35元.现在小李要将购进的60盒弥猴桃分配给每个店铺各30盒,设分配给甲店精品盒a盒,请你根据题意填写下表:
| 精品盒数量(盒) | 普通盒数量(盒) | 合计(盒) | |
| 甲店 | a | 30-a | 30 |
| 乙店 | 35-a | a-5 | 30 |
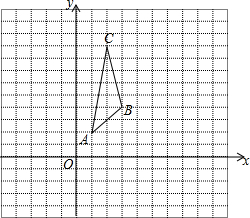 在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).
在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(1,2),B(3,4),C(2,9).