题目内容
如图，梯形ABCD中，AD∥BC，对角线BD恰好平分∠ABC，那么图中可以证明一定相等的两条线段是（ ）| A、AB=CD |
| B、AD=CD |
| C、AB=AD |
| D、BD=BC |
考点：梯形,等腰三角形的判定与性质
专题：
分析：分别利用角平分线的性质以及平行线的性质得出∠ABD=∠ADB，进而得出AB=AD．
解答：证明：∵AD∥BC，对角线BD恰好平分∠ABC，
∴∠ADB=∠DBC，∠ABD=∠DBC，
∴∠ABD=∠ADB，
∴AB=AD．
故选：C．
∴∠ADB=∠DBC，∠ABD=∠DBC，
∴∠ABD=∠ADB，
∴AB=AD．
故选：C．
点评：此题主要考查了角平分线的性质以及平行线的性质等知识，得出∠ABD=∠ADB是解题关键．
练习册系列答案
相关题目
【问题情境】
如图，已知直线AB、DE相交于点O，∠AOC=160°，OC平分∠EOB，试求∠AOD的度数．下列说法中正确的是（ ）
| A、若|a|=|b|，则a=b |
| B、若ac=bc，则a=b |
| C、若线段AC=BC，则点C是线段AB的中点 |
| D、过n边形的一个顶点有（n-3）条对角线 |
如图，已知点A，B的坐标分别为A（5.5，12），B（10.5，0），若P是y轴上一动点，求△ABP周长的最小值．
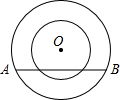如图，以O为圆心的两个同心圆中，半径分别为3和5，若大圆的弦AB与小圆相交，则弦AB的长的取值范围是（ ）| A、8≤AB≤10 |
| B、8＜AB＜10 |
| C、8＜AB≤10 |
| D、6≤AB≤10 |
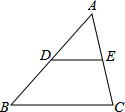如图，在△ABC中，D、E分别是AB、AC的中点，若△ABC的面积为