题目内容
 如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值.
如图,已知点A,B的坐标分别为A(5.5,12),B(10.5,0),若P是y轴上一动点,求△ABP周长的最小值.考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:先根据已知条件求出AB的长,再根据P为x轴上一动点,确定出P点的位置,即可求出BP+AP的长,最后即可求出△ABP周长的最小值.
解答: 解:做点A关于y轴的对称点A′,连接A′B,当点P运动到A′B与y轴的交点时,△ABP周长的最小值.
解:做点A关于y轴的对称点A′,连接A′B,当点P运动到A′B与y轴的交点时,△ABP周长的最小值.
∵A(5.5,12),B(10.5,0),
∴AB=
=13,A′(-5.5,12),
又∵P为y轴上一动点,
当求△ABP周长的最小值时,
∴A′B=
=20,
∴△ABP周长的最小值为:AB+A′B=13+20=33.
 解:做点A关于y轴的对称点A′,连接A′B,当点P运动到A′B与y轴的交点时,△ABP周长的最小值.
解:做点A关于y轴的对称点A′,连接A′B,当点P运动到A′B与y轴的交点时,△ABP周长的最小值.∵A(5.5,12),B(10.5,0),
∴AB=
| (10,5-5,5)2+(0-12)2 |
又∵P为y轴上一动点,
当求△ABP周长的最小值时,
∴A′B=
| (10.5+5.5)2+(0-12)2 |
∴△ABP周长的最小值为:AB+A′B=13+20=33.
点评:本题主要考查了轴对称-最短路线问题,在解题要结合图形再与各个知识点相结合,找出点P所在的位置是本题的关键.

练习册系列答案
相关题目
 如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )
如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )| A、AB=CD |
| B、AD=CD |
| C、AB=AD |
| D、BD=BC |
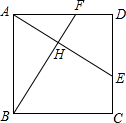 如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H
如图,在正方形ABCD中,E,F分别是边CD,DA上的点,且CE=DF,AE与BF交于点H(1)判断线段AE,BF的位置关系,并说明理由;
(2)找出图中所有与△ABH相似的三角形.(不添加任何辅助线)
已知x=2,y=-1是方程ax+y=3的一组解,则a的值( )
| A、1 | B、2 | C、-1 | D、-2 |
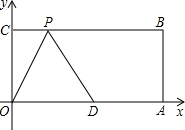 如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为
如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为 如图,将A向右移20个单位长度,再向左移15个单位长度,那么该点表示的数是
如图,将A向右移20个单位长度,再向左移15个单位长度,那么该点表示的数是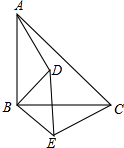 已知:如图,△ABC和△DBE均为等腰直角三角形.
已知:如图,△ABC和△DBE均为等腰直角三角形. 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DE⊥AC,垂足为F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC、AC于D、E两点,过点D作DE⊥AC,垂足为F.