题目内容
如图,在平面直角坐标系中,直线AC,BC交于y轴于点C(0,3),两直线AC,BC分别交轴于A,B两点(OA<OB),且OA,OB的长分别是一元二次方程4x2-25x+36=0的两个根.
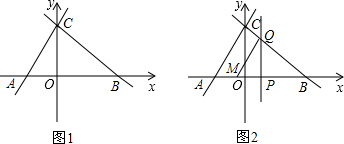
(1)试判断△AOC与△COB是否相似?并说明理由;
(2)点M是线段AB间的一点,过M点作MQ⊥BC于Q,过Q点作垂线交AB于点P,若△PMQ的周长为
,求点P的坐标;
(3)当点P的坐标为P(2,0)时,在直线PQ上是否存在一点N,使△BCN为直角三角形?若存在,直接写出符合条件的N的坐标;若不存在,请说明理由.

(1)试判断△AOC与△COB是否相似?并说明理由;
(2)点M是线段AB间的一点,过M点作MQ⊥BC于Q,过Q点作垂线交AB于点P,若△PMQ的周长为
| 27 |
| 4 |
(3)当点P的坐标为P(2,0)时,在直线PQ上是否存在一点N,使△BCN为直角三角形?若存在,直接写出符合条件的N的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据解一元二次方程,可得A、B点坐标,根据两边对应成比例且夹角相等的两个三角形相似,可得答案;
(2)根据余角的性质,可得∠OQP=∠B,根据两角对应相等的两个三角形相似,可得△MQP∽△BOC,再根据相似三角形的性质,可得PQ的长,再根据平行于三角形的一边与其它两边相交得到的三角形相似,可得△BPQ∽△BOC,根据相似三角形的性质,可得BP的长,再根据线段的和差,可得OP的长;
(3)根据勾股定理,可得直角三角形三边的关系:分类讨论:当BN2+CN2=BC2时,当BC2+CN2=BN2时,当BC2+BN2=CN2时,可得方程,根据解方程,可得答案.
(2)根据余角的性质,可得∠OQP=∠B,根据两角对应相等的两个三角形相似,可得△MQP∽△BOC,再根据相似三角形的性质,可得PQ的长,再根据平行于三角形的一边与其它两边相交得到的三角形相似,可得△BPQ∽△BOC,根据相似三角形的性质,可得BP的长,再根据线段的和差,可得OP的长;
(3)根据勾股定理,可得直角三角形三边的关系:分类讨论:当BN2+CN2=BC2时,当BC2+CN2=BN2时,当BC2+BN2=CN2时,可得方程,根据解方程,可得答案.
解答:解:(1)相似,理由如下:
4x2-25x+36=0,
解得x1=4,x2=
,
OA<OB,得A(-
,0),B(4,0),即OA=
,OB=4.
∵OC=3,
∴
=
=
,
=
,
=
,∠AOC=∠COB,
∴△AOC∽△COB;
(2)由MQ⊥BC于Q,得∠OQB=90°,
Q点作垂线交AB于点P,得∠QPO=90°,
∠OQP=∠B,∠QPO=∠OQB,
∴△MQP∽△BOC,
∴
=
,
=
,
解得PQ=
,
PQ∥OC,
∴△BPQ∽△BOC,
∴
=
即
=
,解得BP=3,
OP=OB-BP=4-3=1,
即P(1,0);
(3)设N点坐标为(2,b),
①当BN2+CN2=BC2时,[(4-2)2+b2]+[22+(3-b)2]=32+42,
化简,得b2-3b-4=0,解得b1=4,b2=-1,
即N1(2,4),N2(2,-1),
②当BC2+CN2=BN2时,[22+(3-b)2]+(32+42)=(4-2)2+b2,
化简,得6b=34解得b=
,即N3(2,
),
③当BC2+BN2=CN2时,(32+42)+[(4-2)2+b2]=22+(3-b)2,
化简,得-6b=16,解得b=-
,即N4(2,-
),
4x2-25x+36=0,
解得x1=4,x2=
| 9 |
| 4 |
OA<OB,得A(-
| 9 |
| 4 |
| 9 |
| 4 |
∵OC=3,
∴
| OA |
| OC |
| ||
| 3 |
| 3 |
| 4 |
| OC |
| OB |
| 3 |
| 4 |
| OA |
| OC |
| OC |
| OB |
∴△AOC∽△COB;
(2)由MQ⊥BC于Q,得∠OQB=90°,
Q点作垂线交AB于点P,得∠QPO=90°,
∠OQP=∠B,∠QPO=∠OQB,
∴△MQP∽△BOC,
∴
| C△MCP |
| C△AOC |
| PQ |
| OB |
| ||
| 3+4+5 |
| PQ |
| 4 |
解得PQ=
| 9 |
| 4 |
PQ∥OC,
∴△BPQ∽△BOC,
∴
| BP |
| OB |
| ||
| 3 |
| BP |
| 4 |
| ||
| 3 |
OP=OB-BP=4-3=1,
即P(1,0);
(3)设N点坐标为(2,b),
①当BN2+CN2=BC2时,[(4-2)2+b2]+[22+(3-b)2]=32+42,
化简,得b2-3b-4=0,解得b1=4,b2=-1,
即N1(2,4),N2(2,-1),
②当BC2+CN2=BN2时,[22+(3-b)2]+(32+42)=(4-2)2+b2,
化简,得6b=34解得b=
| 17 |
| 3 |
| 17 |
| 3 |
③当BC2+BN2=CN2时,(32+42)+[(4-2)2+b2]=22+(3-b)2,
化简,得-6b=16,解得b=-
| 8 |
| 3 |
| 8 |
| 3 |
点评:本题考查了一次函数综合题,(1)利用了两边对应成比例且夹角相等的两个三角形相似,(2)利用了两角对应相等的两个三角形相似,相似三角形周长的比等于相似比,平行线截三角形的两边所得的三角形与原三角形相似,(3)利用了勾股定理得出方程是解题关键,注意要分类讨论,以防遗漏.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 将一副直角三角尺如图所示,叠放在一起,则
将一副直角三角尺如图所示,叠放在一起,则| BE |
| CE |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )
如图,梯形ABCD中,AD∥BC,对角线BD恰好平分∠ABC,那么图中可以证明一定相等的两条线段是( )| A、AB=CD |
| B、AD=CD |
| C、AB=AD |
| D、BD=BC |
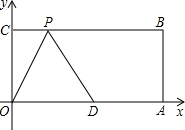 如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为
如图,四边形OABC是矩形,点A、C的坐标分别为A(10,0),C(0,4),点D是OA的中点,点P在BC边上运动.当△ODP是腰长为5的等腰三角形时,点P的坐标为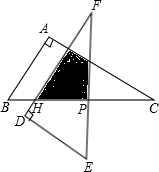 如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为
如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为 如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC
如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC