题目内容
14.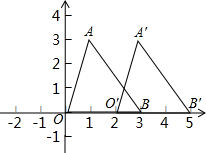 如图,三角形AOB的顶点A,B的坐标分别为(1,3),(3,0),经过平移,三角形AOB变成了三角形A′O′B′,其中点O′的坐标为(2,0),试写出点A′,B′的坐标,平面上任一点P(x,y)在这个平移下的像为点P′(x′,y′),试问:点P′的坐标与点P的坐标之间有什么关系呢?
如图,三角形AOB的顶点A,B的坐标分别为(1,3),(3,0),经过平移,三角形AOB变成了三角形A′O′B′,其中点O′的坐标为(2,0),试写出点A′,B′的坐标,平面上任一点P(x,y)在这个平移下的像为点P′(x′,y′),试问:点P′的坐标与点P的坐标之间有什么关系呢?
分析 根据O(0,0)经过平移得到点O′的坐标为(2,0),于是得到平移的规律是△ABC沿x轴的正方向平移了2个单位长度,即平移前后对应点的坐标的关系是横坐标加2,纵坐标不变,于是得到结果.
解答 解:∵经过平移,点O′的坐标为(2,0),
∴△ABC沿x轴的正方向平移了2个单位长度,
∵A,B的坐标分别为(1,3),(3,0),
∴1+2=3,3+2=5,
∴A′(3,3),B′(5,0),
∵点P(x,y)在这个平移下的像为点P′(x′,y′),
∴x+2=x′,y=y′,
∴点P′的坐标与点P的坐标之间的关系为:x+2=x′,y=y′.
点评 本题考查了坐标与图形变化-平移,找准平移的规律是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.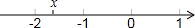 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
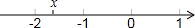 实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )
实数x在数轴上位置如图,则x0,x-1,x-2,x-4的大小关系为( )| A. | x0>x-1>x-2>x-4 | B. | x-4>x-2>x-1>x0 | C. | x-2>x-4>x0>x-1 | D. | x0>x-2>x-4>x-1 |
15.数32009×72010×132011的个位数字是( )
| A. | 1 | B. | 3 | C. | 7 | D. | 9 |
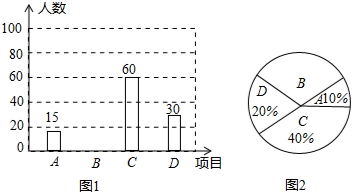
 如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.
如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.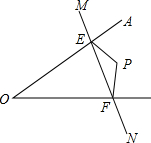 如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.
如图,点P在∠AOB内部,点M,N分别是点P关于直线AO、BO的对称点,若△PEF的周长为15,求MN的长.
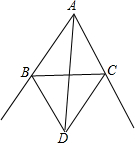 如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.
如图,已知,△ABC的∠B,∠C的外角平分线交于点D,AD是∠BAC的平分线吗?说明理由.