题目内容
9.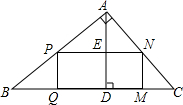 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要使它加工成矩形零件PQMN,使矩形的一边在BC上,其他两个顶点分别在AB、AC上,并且PN=2PQ,PN的长是多少?
分析 根据矩形的性质得PN∥QM,设PQ=x,则PN=2x,ED=x,AE=AD-ED=80-x,然后利用PN∥BC判断△APN∽△ABC,则根据相似三角形的性质得$\frac{80-x}{80}$=$\frac{2x}{120}$,再利用比例性质计算出x即可得到PN的长.
解答 解:∵四边形PQMN为矩形,
∴PN∥QM,
∵AD为高,
∴四边形PQDE为矩形,
∴ED=PQ,
设PQ=x,则PN=2x,ED=x,AE=AD-ED=80-x,
∵PN∥BC,
∴△APN∽△ABC,
∴$\frac{AE}{AD}$=$\frac{PN}{BC}$,即$\frac{80-x}{80}$=$\frac{2x}{120}$,
解得x=$\frac{240}{7}$,
∴PN=2x=$\frac{480}{7}$.
答:PN的长是$\frac{480}{7}$m.
点评 本题考查了相似三角形的应用:利用相似三角形的性质即相似三角形的对应边的比相等计算线段的长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.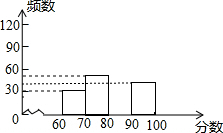 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
请根据以上图表提供的信息,解答下列问题:
(1)表中m的值为200,n的值为0.25;
(2)补全频数分布直方图;
(3)测试成绩的中位数落在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约有多少人?
 某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:
某中学组织全校1500名学生参加安全知识测试,为了解本次测试成绩的分别情况,从中随机抽取了部分学生的成绩,绘制出如图不完整的统计图表:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 50 | n |
| 80≤x<90 | 80 | 0.4 |
| 90≤x<100 | 40 | 0.2 |
| 合计 | m | 1 |
(1)表中m的值为200,n的值为0.25;
(2)补全频数分布直方图;
(3)测试成绩的中位数落在哪个分数段?
(4)规定测试成绩80分以上(含80分)为合格,请估计全校学生中合格人数约有多少人?
14. 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
 如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )
如图,AD是正五边形ABCDE的一条对角线,则∠BAD等于( )| A. | 72° | B. | 108° | C. | 36° | D. | 62° |
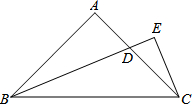 等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.
等腰直角三角形ABC中,∠A=90°,∠B的平分线交AC于D,过点C向BD作垂线,并与BD延长线交于点E,求证:BD=2CE.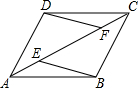 已知,如图,在四边形ABCD中,AB=CD,AD=BC,点E、F在AC上,且AE=CF.图中有哪些三角形全等?请分别加以证明.
已知,如图,在四边形ABCD中,AB=CD,AD=BC,点E、F在AC上,且AE=CF.图中有哪些三角形全等?请分别加以证明.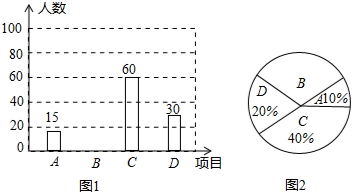
 如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.
如图,在△ABC中,∠ABC=90°,D为AB延长线上一点,点E在BC边上且BE=BD,连结AE、DE、DC,AE=DC.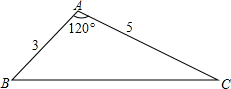 已知:如图所示,求BC、tanB.
已知:如图所示,求BC、tanB.