题目内容
15.等腰三角形的腰上的高线与底边的夹角为45°,若底边上的高为5,则此等腰三角形的面积为( )| A. | 5 | B. | 10 | C. | 20 | D. | 25 |
分析 由题意可得等腰三角形一腰上的高与底边的夹角为45°,根据直角三角形的两个锐角互余可以得到该等腰三角形的底角是45°,等腰三角形腰上的高与底边的夹角等于顶角的一半,求出顶角的度数,从而判断三角形是等腰直角三角形,根据直角三角形斜边的中线的性质求得底边的长,根据面积公式即可求得.
解答 解:∵若等腰三角形一腰上的高与底边的夹角为45°,
又∵等腰三角形的两个底角相等,
∴该等腰三角形的底角是45°,
∴顶角等于90°,
∴该三角形一定是等腰直角三角形.
∴底边的高就是底边的中线,
∵底边的高为5,
∴底边的长为10,
∴此等腰三角形面积=$\frac{1}{2}$×10×5=25.
故选D.
点评 本题主要考查等腰三角形的性质及直角三角形的判定和性质以及三角形的面积,证得三角形是直角三角形是本题的关键.

练习册系列答案
相关题目
3.已知xm=a,xn=b,那么x3m+2n的值等于( )
| A. | 3a+2b | B. | a3+b2 | C. | a3b2 | D. | a3mb2n |
10.-(-3)的相反数的倒数是( )
| A. | -$\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | -3 |
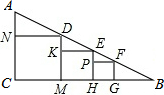 如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
如图,在Rt△ABC中,∠C=90°,从左向右依次作正方形CNDM,正方形MKEH,正方形HPFG.已知正方形CNDM的边长为10,正方形MKEH的边长为8.
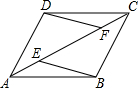 已知,如图,在四边形ABCD中,AB=CD,AD=BC,点E、F在AC上,且AE=CF.图中有哪些三角形全等?请分别加以证明.
已知,如图,在四边形ABCD中,AB=CD,AD=BC,点E、F在AC上,且AE=CF.图中有哪些三角形全等?请分别加以证明.
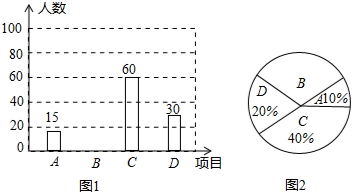
 如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.
如图,是我国体育健儿在最近六届奥运会上获得奖牌的情况,那么我国体育健儿在这六届奥运会上共获得的奖牌数为286枚.