题目内容
 如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为
如图,把矩形ABCO放置在平面直角坐标系中,O为坐标原点,B的坐标为(8,6),A、C分别在坐标轴上,P是线段BC上动点,设PC=m,已知点D在第一象限,且是直线y=2x+6上的一点,若△APD是等腰直角三角形,则点D的坐标为考点:等腰三角形的判定,一次函数图象上点的坐标特征
专题:
分析:作DE⊥y轴于E点,作PF⊥y轴于F点,可得∠DEA=∠AFP=90°,再由三角形ADP为等腰直角三角形,得到AD=AP,利用同角的余角相等得到一对角相等,利用AAS得到三角形ADE与三角形APF全等,由全等三角形的对应边相等得到AE=PF,由AE+OA求出OE的长,即为D的纵坐标,代入直线解析式求出D的横坐标,即可确定出D的坐标;
解答:解:(1)如图1所示,作DE⊥y轴于E点,作PF⊥y轴于F点,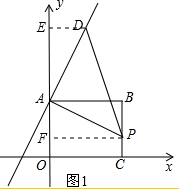 可得∠DEA=∠AFP=90°,
可得∠DEA=∠AFP=90°,
∵△DAP为等腰直角三角形,
∴AD=AP,∠DAP=90°,
∴∠EAD+∠DAB=90°,∠DAB+∠BAP=90°,
∴∠EAD=∠BAP,
∵AB∥PF,
∴∠BAP=∠FPA,
∴∠EAD=∠FPA,
∵在△ADE和△PAF中,
∴△ADE≌△PAF(AAS),
∴AE=PF=8,DE=AF,OE=OA+AE=14,
设点D的横坐标为x,由14=2x+6,得x=4,
∴点D的坐标是(4,14),DE=AF=BP=4,
∴PC=6-4=2,
∴m=2;
故答案为:(4,14);2.
 可得∠DEA=∠AFP=90°,
可得∠DEA=∠AFP=90°,∵△DAP为等腰直角三角形,
∴AD=AP,∠DAP=90°,
∴∠EAD+∠DAB=90°,∠DAB+∠BAP=90°,
∴∠EAD=∠BAP,
∵AB∥PF,
∴∠BAP=∠FPA,
∴∠EAD=∠FPA,
∵在△ADE和△PAF中,
|
∴△ADE≌△PAF(AAS),
∴AE=PF=8,DE=AF,OE=OA+AE=14,
设点D的横坐标为x,由14=2x+6,得x=4,
∴点D的坐标是(4,14),DE=AF=BP=4,
∴PC=6-4=2,
∴m=2;
故答案为:(4,14);2.
点评:此题考查了一次函数综合题,涉及的知识有:全等三角形的判定与性质,等腰直角三角形的性质,一次函数图象上点的坐标特征,培养学生综合运用知识进行推理论证和计算的能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 数轴上点A表示的数可能是( )
数轴上点A表示的数可能是( )| A、4的算术平方根 | |||
B、
| |||
C、
| |||
| D、8的立方根 |
已知∠AOB是平角,过点O作射线OC将∠AOB分成∠AOC和∠BOC,若∠AOC<∠BOC,则∠BOC是( )
| A、锐角 | B、直角 |
| C、钝角 | D、无法确定 |
已知Rt△ABC三个顶点均在函数y=x2上,斜边与x轴平行,则顶点到斜边上高的取值范围为( )
| A、h=1 | B、0<h<1 |
| C、1<h≤2 | D、h>2 |
 如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证:
如图,大圆O1的半径O1A是小圆O2的直径,⊙O1的另一半O1C交⊙O2于B.求证:
 如图,等边三角形的边长是6,求:
如图,等边三角形的边长是6,求: 已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由.
已知:如图,∠1=∠2,∠C=∠D,请由此找出所有互相平行的直线,并说明理由. 如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径.
如图,一个旅游船从大桥AB的P处前往山脚下的Q处接游客,然后送往河岸BC上,再回到P处,请画出旅游船的最短路径. 如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.
如图,P为等腰三角形ABC的底边AB上的任意一点,PE⊥AC于点E,PF⊥BC于点F,AD⊥BC于点D.求证:PE+PF=AD.