题目内容
7.平面直角坐标系内,点A(1+a,1-a)一定不在第二象限.分析 本题可转化为解不等式组的问题,求出无解的不等式即可.
解答 解:由题意可得:
$\left\{\begin{array}{l}{1+a>0}\\{1-a>0}\end{array}\right.$
$\left\{\begin{array}{l}{1+a<0}\\{1-a<0}\end{array}\right.$,、
$\left\{\begin{array}{l}{1+a>0}\\{1-a<0}\end{array}\right.$、
$\left\{\begin{array}{l}{1+a<0}\\{1-a>0}\end{array}\right.$,
解这四组不等式可知$\left\{\begin{array}{l}{1+a<0}\\{1-a>0}\end{array}\right.$无解,
因而点A的横坐标是负数,纵坐标是正数,不能同时成立,即点A一定不在第二象限,
故答案为二.
点评 本题主要考查平面直角坐标系中各象限内点的坐标的符号,把符号问题转化为解不等式组的问题.

练习册系列答案
相关题目
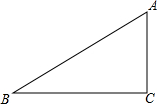 已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.
已知Rt△ABC中,AC=3,BC=4,翻折使点A和B点重合,尺规作图,画出折痕,折痕交△ABC的两边于点E、F,求EF的长度.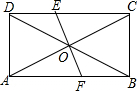 如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF.
如图,在矩形ABCD中,已知AC、BD相交于O,EF⊥AC于O,且交AB于F,交CD于E,EF=AF. 如图,在方格纸中有三个点A、B、C,若点A的位置记为(0,1),点B的位置记为(2,-1),则点C的位置应记为(-3,-2).
如图,在方格纸中有三个点A、B、C,若点A的位置记为(0,1),点B的位置记为(2,-1),则点C的位置应记为(-3,-2).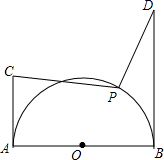 如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.
如图,半圆的半径为1,AB为直径,AC、BD为切线,AC=1,BD=2,P为$\widehat{AB}$上一动点,求$\frac{\sqrt{2}}{2}$PC+PD的最小值.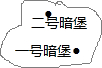 如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.
如图为某战役缴获敌人防御工事坐标地图碎片,依稀可见一号暗堡坐标为(1,2),二号暗堡坐标为(-3,2),另由情报得知,指挥部坐标为(-1,-2),你能在图上际出指挥部的位置P吗?试通过画图加以说明.