题目内容
15.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.已知直角三角形的两直角边分别为5和12,则它的最小覆盖圆的半径的值为6.5.分析 最小覆盖圆就是三角形的外接圆;利用勾股定理可以求得该直角三角形的斜边长为13,然后由“直角三角形的外接圆是以斜边中点为圆心,斜边长的一半为半径的圆”来求该直角三形外接圆半径.
解答 解:∵直角三角形的两条直角边分别为5和12,
∴根据勾股定理知,该直角三角的斜边长为$\sqrt{{5}^{2}+1{2}^{2}}$=13;
∴其外接圆半径长为6.5;
∴最小覆盖圆的半径的值为6.5,
故答案是:6.5.
点评 本题考查了三角形的外接圆与外心、勾股定理.直角三角形的外接圆半径为斜边边长的一半.

练习册系列答案
相关题目
20. 如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
(1)若∠BAC=70°,∠D=40°,求∠CED的度数;
(2)试问BD与ID相等吗?为什么?
 如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.
如图,点I是三角形ABC的内心,连接AI并延长交BC于点E,交三角形ABC的外接圆于点D,连接BD.(1)若∠BAC=70°,∠D=40°,求∠CED的度数;
(2)试问BD与ID相等吗?为什么?
7.A,B两地果园分别有苹果20吨和30吨,C,D两地分别需要苹果15吨和35吨.
(1)若从A果园运到C地的苹果为x吨,请用含x的式子填写下表:
(2)已知从A,B到C,D的运价如下表:
求用含x的式子表示出总运输费,并进行化简.
(1)若从A果园运到C地的苹果为x吨,请用含x的式子填写下表:
| 到C地 | 到D地 | |
| A果园 | x吨 | (20-x)吨 |
| B果园 | (15-x)吨 | (15+x)吨 |
| 到C地 | 到D地 | |
| A果园 | 每吨15元 | 每吨12元 |
| B果园 | 每吨10元 | 每吨9元 |
4. 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )
 实数a,b在数轴上的位置如图所示,以下说法正确的是( )
实数a,b在数轴上的位置如图所示,以下说法正确的是( )| A. | a+b=0 | B. | ab>0 | C. | b<a | D. | |b|<|a| |
 一个边长为4的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E.
一个边长为4的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E.
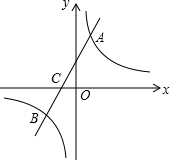 如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.
如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象交于A,B两点,与x轴交于C点,已知点A的坐标为(n,6),点C的坐标为(-2,0),且tan∠ACO=2.