Question

5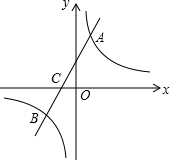．如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=$\frac{m}{x}$（m≠0）的图象交于A，B两点，与x轴交于C点，已知点A的坐标为（n，6），点C的坐标为（-2，0），且tan∠ACO=2．
（1）求该反比例函数和一次函数的解析式；
（2）求点B的坐标；
（3）请利用图象直接写出不等式$\frac{m}{x}$＞kx+b的解集．

Answer 1

分析 （1）利用正切函数求得A（ 1，6），然后利用待定系数法即可求得．
（2）联立方程，解方程组即可求得B的坐标；
（3）根据函数的图象和交点坐标即可求得．

解答 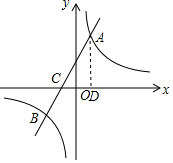解：（1）过A作AD垂直x轴于点D，
∵A的坐标为（n，6），
∴AD=6
在Rt△ACD中，tan∠ACO=2，
∴$\frac{AD}{CD}$=2，
解得：n=1
∴A的坐标为（1，6），
又∵A在反比例函数y=$\frac{m}{x}$（m≠0）的图象上，
∴m=6，
∵一次函数y=kx+b过A（1，6）和C（-2，0），
∴$\left\{\begin{array}{l}{6=k+b}\\{0=-2k+b}\end{array}\right.$解得：$\left\{\begin{array}{l}{k=2}\\{b=4}\end{array}\right.$
∴一次函数解析式为y=2x+4．
∴反比例函数解析式为：y=$\frac{6}{x}$，一次函数解析式为：y=2x+4．
（2）解方程组：$\left\{\begin{array}{l}{y=\frac{6}{x}}\\{y=2x+4}\end{array}\right.$解得：x₁=1（舍去），x₂=-3，
∴B的坐标为（-3，-2）．
（3）不等式$\frac{m}{x}$＞kx+b的解集为：x＜-3或0＜x＜1．

点评 此题考查了反比例函数与一次函数的交点问题．其知识点有解直角三角形，待定系数法求解析，解方程组等，此题难度适中，注意掌握数形结合思想与方程思想的应用．