题目内容
如图，AB∥CD，AC与BD交于点O，BO：OD=1：3，则△ABO与△CDO的周长比为考点：相似三角形的判定与性质
专题：探究型
分析：先根据相似三角形的判定定理得出△AOB∽△COD，再根据相似三角形周长的比等于相似比进行解答．
解答：解：∵AB∥CD，
∴∠B=∠D，∠A=∠C，
∴△ABO∽△CDO，
∵BO：OD=1：3，
∴L△ABO：L△CDO=1：3．
故答案为：1：3．
∴∠B=∠D，∠A=∠C，
∴△ABO∽△CDO，
∵BO：OD=1：3，
∴L△ABO：L△CDO=1：3．
故答案为：1：3．
点评：本题考查的是相似三角形的判定与性质，熟知相似三角形周长的比等于相似比是解答此题的关键．
练习册系列答案
百年学典课时学练测系列答案
相关题目
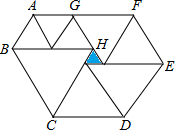如图，是由9个等边三角形（三条边都相等的三角形）组成的装饰图案，已知中间最小的等边三角形（阴影部分）边长为1cm，现欲将此图案的周边镶上一根彩线，问彩线至少需要多长？
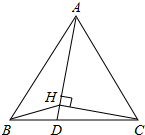在等边△ABC边BC上取一点D，使BD：DC=1：2，作CH⊥AD于H，连接BH，求证：∠DBH=∠DAB．若四个互不相等的正实数a，b，c，d满足（a2012-c2012）（a2012-d2012）=2012，（b2012-c2012）（b2012-d2012）=2012，则（ab）2012-（cd）2012的值为（ ）
| A、-2012 | B、-2011 |
| C、2012 | D、2011 |