题目内容
将一长方形切去一角后得一边长分别是13、19、20、25和31的五边形(顺序不一定按此).则此五边形的面积为 .
考点:面积及等积变换
专题:计算题,转化思想
分析:根据题意可知,切去的是一个直角三角形,如图,长方形的面积-直角三角形的面积=五边形的面积;
解答: 解:根据题意得,被切去的是一个直角三角形,则
解:根据题意得,被切去的是一个直角三角形,则
①当斜边等于13时,而52+122=132,20+5=25,19+12=31成立,所以两对平行的边分别是20、25,19、31,斜边是13;
②当斜边等于19时,而192不能表示为两个平方数的和,因此不可能是19;
③当斜边等于20时,而122+162=202,但是无法找出两对边,它们的差分别是12和16;
④当斜边等于25时,而72+242=252,但是仍然无法找出两对满足要求的边;
⑤当斜边等于31时,312不能表示为两个平方数的和;
综上如右图,五边形的面积为:31×25-
×12×5=745;
故答案为:745.
 解:根据题意得,被切去的是一个直角三角形,则
解:根据题意得,被切去的是一个直角三角形,则①当斜边等于13时,而52+122=132,20+5=25,19+12=31成立,所以两对平行的边分别是20、25,19、31,斜边是13;
②当斜边等于19时,而192不能表示为两个平方数的和,因此不可能是19;
③当斜边等于20时,而122+162=202,但是无法找出两对边,它们的差分别是12和16;
④当斜边等于25时,而72+242=252,但是仍然无法找出两对满足要求的边;
⑤当斜边等于31时,312不能表示为两个平方数的和;
综上如右图,五边形的面积为:31×25-
| 1 |
| 2 |
故答案为:745.
点评:本题主要考查了多边形的面积变换,正确分析、画出图形是解答的关键,体现了转化思想.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
比较
,
,
的大小,正确的是( )
| 3 | 3 |
| 3 |
| 2 |
| 5 |
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、
|
气象台预报:“本市明天降水概率是80%”,但据经验,气象台预报的准确率仅为80%,则在此经验下,本市明天降水的概率为( )
| A、84% | B、80% |
| C、68% | D、64% |
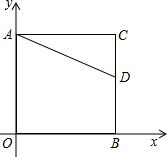 如图,正方形AOBC的B点在x轴正半轴上,A在y轴正半轴上,边长为
如图,正方形AOBC的B点在x轴正半轴上,A在y轴正半轴上,边长为 如图,AB∥CD,AC与BD交于点O,BO:OD=1:3,则△ABO与△CDO的周长比为
如图,AB∥CD,AC与BD交于点O,BO:OD=1:3,则△ABO与△CDO的周长比为