题目内容
若一个三角形的三边长a、b、c满足(a-1)2+(b-1)2+c2=2c-1,你能根据已知条件判断这个三角形的形状吗?
考点:因式分解的应用
专题:计算题
分析:先移项,再利用完全平方公式得到(a-1)2+(b-1)2+(c-1)2=0,接着根据非负数的性质得a-1=0,b-1=0,c-1=0,则a=b=c=1,于是根据等边三角形的判定即可得到这个三角形为等边三角形.
解答:解:∵(a-1)2+(b-1)2+c2=2c-1,
∴(a-1)2+(b-1)2+(c-1)2=0,
∴a-1=0,b-1=0,c-1=0,
∴a=b=c=1,
∴这个三角形为等边三角形.
∴(a-1)2+(b-1)2+(c-1)2=0,
∴a-1=0,b-1=0,c-1=0,
∴a=b=c=1,
∴这个三角形为等边三角形.
点评:本题考查了因式分解的应用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
相关题目
△ABC,若AB=12,BC=16,AC=20,点D,E,F分别为AB,BC,AC的中点,则△DEF的面积为( )
| A、24 | B、48 | C、96 | D、192 |
抛物线y=x2-2x+3的顶点坐标是( )
| A、(1,2) |
| B、(1,-2) |
| C、(-1,2) |
| D、(-1,-2) |
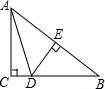 如图,在Rt△ABC中,∠C=90°,DE⊥AB于点E,且AE=BE,当AB=5,AC=3时,求△ACD的周长.
如图,在Rt△ABC中,∠C=90°,DE⊥AB于点E,且AE=BE,当AB=5,AC=3时,求△ACD的周长.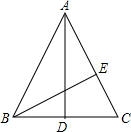 如图,在△ABC中,AB=AC=17,BC=16,AD为中线,BE⊥AC,垂足为E,则AD=
如图,在△ABC中,AB=AC=17,BC=16,AD为中线,BE⊥AC,垂足为E,则AD=