题目内容
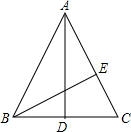如图，在△ABC中，AB=AC=17，BC=16，AD为中线，BE⊥AC，垂足为E，则AD=考点：勾股定理,等腰三角形的性质
专题：
分析：先根据等腰三角形的性质求出BD的长，再根据勾股定理求出AD的长即可；根据sinC=
=
即可得出BE的长．
| AD |
| AC |
| BE |
| BC |
解答：解：∵在△ABC中，AB=AC=17，BC=16，AD为中线，
∴AD⊥BC，BD=
BC=8，
∴AD=
=
=15．
∵sinC=
=
，
∴
=
，解得BE=
．
故答案为：15，
．
∴AD⊥BC，BD=
| 1 |
| 2 |
∴AD=
| AB2-BD2 |
| 172-82 |
∵sinC=
| AD |
| AC |
| BE |
| BC |
∴
| 15 |
| 17 |
| BE |
| 16 |
| 240 |
| 17 |
故答案为：15，
| 240 |
| 17 |
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
如图，数a、b、c在数轴上对应的点分别为A、B、C，你能去掉绝对值符号并合并同类项吗？
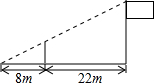如图，小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（ ）| A、10m | B、9m | C、8m | D、7m |
下列解方程中，变形正确的是（ ）
| A、由3x-2=1得3x=1-2 | ||||
B、由-2x=3得x=
| ||||
C、
| ||||
| D、由3（x-2）=1得3x-2=1 |
下列各组式子中是同类项的是（ ）
| A、a2与2a |
| B、a与-a |
| C、ab与a+b |
| D、3xy与3ab |
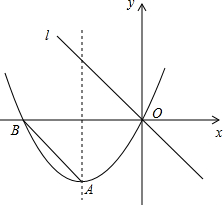如图，对称轴为x=-3的抛物线y=ax2+2x 与x 轴相交于点B、O．连结AB，把AB所在的直线平移，使它经过原点O，得到直线l（1）①求抛物线的解析式，并求出顶点A 的坐标；