题目内容
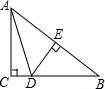如图，在Rt△ABC中，∠C=90°，DE⊥AB于点E，且AE=BE，当AB=5，AC=3时，求△ACD的周长．考点：勾股定理,线段垂直平分线的性质
专题：
分析：先根据勾股定理求出BC的长，再根据DE⊥AB于点E，且AE=BE可得出AD=BD，进而可得出结论．
解答：解：∵在Rt△ABC中，∠C=90°，AB=5，AC=3，
∴BC=
=4．
∵DE⊥AB于点E，且AE=BE，
∴AD=BD，
∴△ACD的周长=AC+BC=3+4=7．
∴BC=
| 52-32 |
∵DE⊥AB于点E，且AE=BE，
∴AD=BD，
∴△ACD的周长=AC+BC=3+4=7．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
一卷搞定系列答案
名校作业本系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
下列命题是真命题的是（ ）
| A、对角线相等的矩形是正方形 |
| B、斜坡的坡度指的是坡角的度数 |
| C、所有的等腰直角三角形都相似 |
| D、顺次连接平行四边形各边中点得到的四边形是菱形 |