题目内容
已知关于x的多项式（a-1）x2+x|a+2|-2x+b，问是否存在实数a，b，使得这个多项式为二次三项式？若存在，请求出a，b的值，若不存在，请说明理由．
考点：多项式
专题：
分析：利用二次三项式的定义求解即可．
解答：解：若（a-1）x2+x|a+2|-2x+b，是二次三项式，
可得a=-1，b≠0或a=-3，b≠0．
所以当a=-1，b≠0或a=-3，b≠0．得（a-1）x2+x|a+2|-2x+b为二次三项式．
可得a=-1，b≠0或a=-3，b≠0．
所以当a=-1，b≠0或a=-3，b≠0．得（a-1）x2+x|a+2|-2x+b为二次三项式．
点评：本题主要考查了多项式，解题的关键熟记多项式的定义，
练习册系列答案
相关题目
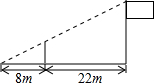如图，小东用长为2.4m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点，此时，竹竿与这一点相距8m，与旗杆相距22m，则旗杆的高为（ ）| A、10m | B、9m | C、8m | D、7m |
下列解方程中，变形正确的是（ ）
| A、由3x-2=1得3x=1-2 | ||||
B、由-2x=3得x=
| ||||
C、
| ||||
| D、由3（x-2）=1得3x-2=1 |