题目内容
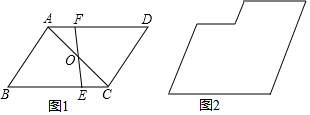
16．
如图：在矩形ABCD中，AB=4，BC=8，对角线AC、BD相交于点O，过点O作OE垂直AC交AD于点E，则DE的长是3．
分析 连接CE，设DE=x，则AE=8-x，判断出OE是AC的垂直平分线，即可推得CE=AE=8-x，然后在Rt△CDE中，根据勾股定理，求出DE的长是多少即可．
解答 解：如图，连接CE，
，
设DE=x，则AE=8-x，
∵OE⊥AC，且点O是AC的中点，
∴OE是AC的垂直平分线，
∴CE=AE=8-x，
在Rt△CDE中，
x2+42=（8-x）2
解得x=3，
∴DE的长是3．
故答案为：3．
点评 此题主要考查了矩形的性质、中垂线的性质和勾股定理，熟练掌握矩形的对角线互相平分和中垂线的性质是解题的关键．
练习册系列答案
相关题目
在平面直角坐标系中，直线l：y=x-1与x轴交于点A1，如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn-1，使得点A1、A2、A3、…在直线l上，点C1、C2、C3、…在y轴正半轴上，则点B2017的坐标是（22016，22017-1）．
8．下列各数中，数值相等的是（ ）
| A． | ±4和$\sqrt{16}$ | B． | 2和$\root{3}{-8}$ | C． | |-2|和2 | D． | -2和$\sqrt{（-2）^{2}}$ |