题目内容
7.已知⊙A的半径长为2,⊙B的半径长为5,如果⊙A与⊙B内含,那么圆心距AB的长度可以为( )| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
分析 利用内含圆心距小于两个半径之和确定正确的答案.
解答 解:∵⊙A的半径长为2,⊙B的半径长为5,⊙A与⊙B内含,
∴AB<5-2=3,
A选项符合,
故选A.
点评 本题考查了由数量关系来判断两圆位置关系的方法.设两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.

练习册系列答案
相关题目
18.一个多边形的内角和是720°,这个多边形的边数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是( )
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
2.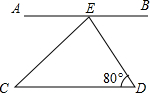 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )
 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
12. 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
 如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )
如图,电线杆AB的中点C处有一标志物,在地面D点处测得标志物的仰角为45°,若测得DC的长度为$\sqrt{2}$a,则电线杆AB的长可表示为( )| A. | a | B. | 2a | C. | $\frac{3}{2}$a | D. | $\frac{5}{2}$a |
19.若x是3的相反数,|y|=4,则x-y的值是( )
| A. | -7 | B. | 1 | C. | -1或7 | D. | 1或-7 |
16.下列实数中,属于无理数的是( )
| A. | -3 | B. | 3.14 | C. | $\frac{2}{7}$ | D. | $\sqrt{2}$ |
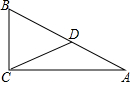 如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.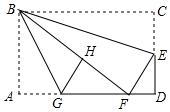 如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG=$\frac{3}{2}$S△FGH.其中正确的是( )
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②AG+DF=FG;③△DEF∽△ABG;④S△ABG=$\frac{3}{2}$S△FGH.其中正确的是( )