题目内容
6.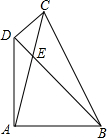 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=6,则AE=2$\sqrt{6}$.
分析 根据锐角三角函数和等积法可以求得BD和BD边上的高的长,从而可以求得AE的长.
解答  解:∵∠CDB=90°,∠DCA=30°,
解:∵∠CDB=90°,∠DCA=30°,
∴∠CED=60°,
∴∠AEB=60°,
作AF⊥BD于点F,
∵∠DAB=90°,AB=6,∠ABD=45°,
∴AB=AD=6,
∴BD=6$\sqrt{2}$,
∴AF=$\frac{AB•AD}{BD}=\frac{6×6}{6\sqrt{2}}=3\sqrt{2}$,
∴AE=$\frac{AF}{sin60°}=\frac{3\sqrt{2}}{\frac{\sqrt{3}}{2}}=2\sqrt{6}$,
故答案为:2$\sqrt{6}$.
点评 本题考查锐角三角函数、勾股定理、等积法,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
12. 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
 如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )
如图,在△ABC中,分别以点A和点B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,若△ABC的周长为24,AB=7,则△ADC的周长为( )| A. | 10 | B. | 17 | C. | 20 | D. | 21.5 |
14.若y=kx+b中,当x=-1时,y=1;当x=2时,y=-2,则k与b为( )
| A. | $\left\{{\begin{array}{l}{k=-1}\\{b=1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{k=-1}\\{b=0}\end{array}}\right.$ | C. | $\left\{\begin{array}{l}k=1\\ b=2\end{array}\right.$ | D. | $\left\{\begin{array}{l}k=1\\ b=-4\end{array}\right.$ |
1. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 甲、乙两人8分钟各跑了800米 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米/分 |
18.一个多边形的内角和是720°,这个多边形的边数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是( )
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
16.下列实数中,属于无理数的是( )
| A. | -3 | B. | 3.14 | C. | $\frac{2}{7}$ | D. | $\sqrt{2}$ |
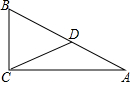 如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.
如图,在Rt△ABC中,∠C=90°,D为AB上的点,BD=CD=5,则AD=5.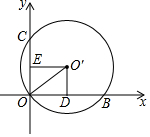 如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )
如图,在平面直角坐标系中,⊙O′经过原点O,并且分别与x轴、y轴交于点B、C,分别作O′E⊥OC于点E,O′D⊥OB于点D.若OB=8,OC=6,则⊙O′的半径为( )