题目内容
10. 问题情境
问题情境已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+$\frac{S}{x}$)(x>0)
探索研究
我们可以借鉴学习函数的经验,先探索函数y=x+$\frac{1}{x}$(x>0)的图象性质.
①列表:
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{4}$ | m | $\frac{5}{2}$ | 2 | $\frac{5}{2}$ | $\frac{10}{3}$ | $\frac{17}{4}$ | … |
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;函数有最小值2;当x>1时,y随x的增大而增大
解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+$\frac{1}{x}$(x>0)的最小值.
y=x+$\frac{1}{x}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$=${(\sqrt{x})}^{2}$+${(\sqrt{\frac{1}{x}})}^{2}$-2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$+2$\sqrt{x}$•$\sqrt{\frac{1}{x}}$=${(\sqrt{x}-\sqrt{\frac{1}{x})}}^{2}$+2
∵${({\sqrt{x}-\sqrt{\frac{1}{x}}})^2}$≥0,∴y≥2
∴当$\sqrt{x}$-$\sqrt{\frac{1}{x}}$=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.
分析 探索研究①计算自变量为$\frac{1}{3}$时的函数值即可得到m值;③如图,利用平滑的曲线顺次连接各点可得到函数图象;④利用函数图象,从最值或增减性写出图象的性质;
解决问题:利用配方法得到y=2($\sqrt{x}$-$\frac{\sqrt{S}}{\sqrt{x}}$)2+4$\sqrt{S}$,然后根据二次函数的性质解决问题.
解答 解:探索研究
①当x=$\frac{1}{3}$时,m=$\frac{1}{3}$+3=$\frac{10}{3}$;
③如图,
④性质:函数有最小值2;当x>1时,y随x的增大而增大;
故答案为$\frac{10}{3}$;函数有最小值2;当x>1时,y随x的增大而增大;
解决问题
y=2(x+$\frac{S}{x}$)=2($\sqrt{x}$-$\frac{\sqrt{S}}{\sqrt{x}}$)2+4$\sqrt{S}$,
当$\sqrt{x}$-$\frac{\sqrt{S}}{\sqrt{x}}$=0时,即x=$\sqrt{S}$,y有最大值4$\sqrt{S}$,
所以该矩形的长为$\sqrt{S}$时,它的周长最小,最小值是4$\sqrt{S}$.
点评 本题考查了二次函数的综合题:从实际问题中分析变量之间的关系,建立函数模型.然后类比二次函数的性质,通过观察、分析、创建,建立直角坐标系下的函数图象,然后数形结合解决问题,需要我们注意的是自变量及函数的取值范围要使实际问题有意义.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
20.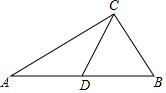 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
1. 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
 甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )
甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )甲、乙两人进行慢跑练习,慢跑路程y(米)与所用时间t(分钟)之间的关系如图所示,下列说法错误的是( )| A. | 前2分钟,乙的平均速度比甲快 | |
| B. | 甲、乙两人8分钟各跑了800米 | |
| C. | 5分钟时两人都跑了500米 | |
| D. | 甲跑完800米的平均速度为100米/分 |
18.一个多边形的内角和是720°,这个多边形的边数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
5. 如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )
如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )
 如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )
如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )| A. | 50° | B. | 60° | C. | 45° | D. | 90° |
15.A、B两地相距480千米,一列慢车从A地出发,每小时行驶60千米,一列快车从B地出发,每小时行驶90千米,快车提前30分钟出发,两车相向而行,慢车行驶多少小时后两车相遇?设慢车行驶x小时后两车相遇,根据题意,下面所列方程正确的是( )
| A. | 60(x+30)+90x=480 | B. | 60x+90(x+30)=480 | ||
| C. | 60(x+$\frac{30}{60}$)+90x=480 | D. | 60x+90(x+$\frac{30}{60}$)=480 |
2.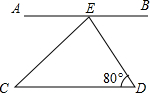 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )
 如图,AB∥CD,CE平分∠AED,则∠C=( )
如图,AB∥CD,CE平分∠AED,则∠C=( )| A. | 40° | B. | 45° | C. | 50° | D. | 55° |
19.若x是3的相反数,|y|=4,则x-y的值是( )
| A. | -7 | B. | 1 | C. | -1或7 | D. | 1或-7 |
20.平面直角坐标系xOy中,⊙A的半径为5,点A的坐标为(2,1),点P的坐标为(0,6),则点P与⊙A的位置关系是( )
| A. | 点P在⊙A外 | B. | 点P在⊙A上 | C. | 点P在⊙A内 | D. | 不能确定 |