题目内容
6.某微店销售甲、乙两种商品,卖出6件甲商品和4件乙商品可获利120元;卖出10件甲商品和6件乙商品可获利190元.(1)甲、乙两种商品每件可获利多少元?
(2)若该微店甲、乙两种商品预计再次进货200件,全部卖完后总获利不低于2300元,已知甲商品的数量不少于120件.请你帮忙设计一个进货方案,使总获利最大.
分析 (1)设甲商品每件获利x元、乙商品每件获利y元,列出方程组即可解决问题.
(2)设甲商品进货a件,总获利为w元,构建一次函数,利用一次函数性质解决问题.
解答 解:(1)设甲商品每件获利x元、乙商品每件获利y元,
由题意,得$\left\{{\begin{array}{l}{6x+4y=120}\\{10x+6y=190}\end{array}}\right.$,解得:$\left\{{\begin{array}{l}{x=10}\\{y=15}\end{array}}\right.$.
答:甲商品每件获利10元,乙商品每件获利15元.
(2)设甲商品进货a件,总获利为w元,
由题意w=10a+15(200-a)=-5a+3000
由-5a+3000≥2300解得:a≤140.
∴a的取值范围为120≤a≤140,且a是整数;
∵-5<0,
∴w随a增大而减小,
∴当a=120时,w最大,此时200-a=80.
∴进货方案为甲商品进货120件,乙商品进货80件.
点评 本题考查一次函数的应用、二元一次方程组的应用等知识,解题的关键是学会设未知数,构建方程组解决问题,学会构建一次函数,利用一次函数性质解决问实际问题中最值问题,属于中考常考题型.

练习册系列答案
相关题目
 已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).
已知抛物线l1:y=-x2+2x+3与x轴交于点A、B(点A在点B左边),与y轴交于点C,抛物线l2经过点A,与x轴的另一个交点为E(4,0),与y轴交于点D(0,-2).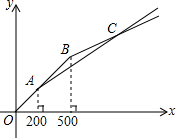 “五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.
“五一”期间,甲、乙两家商店以同样价格销售相同的商品,两家优惠方案分别为:甲店一次性购物中超过200元后的价格部分打七折;乙店一次性购物中超过500元后的价格部分打五折,设商品原价为x元(x≥0),购物应付金额为y元.