题目内容
16．解不等式$\left\{\begin{array}{l}{x+2≤4}\\{\frac{x}{2}+1＞\frac{1}{3}}\end{array}\right.$．分析 分别求出各不等式的解集，再求出其公共解集即可．
解答 解：$\left\{\begin{array}{l}x+2≤4①\\ \frac{x}{2}+1＞\frac{1}{3}②\end{array}\right.$，由①得，x≤2，由②得，x＞-$\frac{4}{3}$．
故不等式组的解集为：-$\frac{4}{3}$＜x≤2．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
相关题目
7．不等式$\frac{1}{3}（x-m）＞2-m$的解集为x＞2，则m的值为（ ）
| A． | 4 | B． | 2 | C． | $\frac{3}{2}$ | D． | $\frac{1}{2}$ |
1．下面分别是四个同学在解方程$\frac{1}{2}$-$\frac{x-3}{3}$=1时的去分母的第一步，其中正确的是（ ）
| A． | 1-2（x-3）=1 | B． | 3-2（x-3）=1 | C． | 1-2（x-3）=6 | D． | 3-2（x-3）=6 |
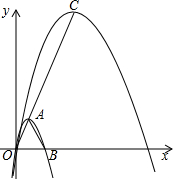如图，抛物线C1：y=-$\sqrt{3}$x2+2$\sqrt{3}$x的顶点为A，与x轴的正半轴交于点B．