题目内容
17.现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:
甲:$\left\{\begin{array}{l}x+y=\\ 12x+8y=\end{array}\right.$; 乙:$\left\{\begin{array}{l}x+y=\\ \frac{x}{12}+\frac{y}{8}=\end{array}\right.$
根据甲、乙两名同学所列的方程组,请你分别指出未知数x、y表示的意义,然后在括号内补全甲、乙两名同学所列的方程组:
甲:x表示A工程队用的时间,y表示B工程队用的时间;
乙:x表示A工程队整治河道的米数,y表示B工程队整治河道的米数.
(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)
分析 (1)根据所列式子可知甲方程所列方程组中未知数为:设A工程队用时x天,B工程队用时y天,乙所列方程组中未知数为:设甲共整治x米,乙共整治y米,据此补全方程组即可;
(2)选择其中一个方程组解答解决问题.
解答 解:(1)甲同学:设A工程队用的时间为x天,B工程队用的时间为y天,由此列出的方程组为$\left\{\begin{array}{l}{x+y=20}\\{12x+8y=180}\end{array}\right.$;
乙同学:A工程队整治河道的米数为x,B工程队整治河道的米数为y,由此列出的方程组为$\left\{\begin{array}{l}{x+y=180}\\{\frac{x}{12}+\frac{y}{8}=20}\end{array}\right.$;
故答案依次为:20,180,180,20,A工程队用的时间,B工程队用的时间,A工程队整治河道的米数,B工程队整治河道的米数;
(2)选甲同学所列方程组解答如下:
$\left\{\begin{array}{l}{x+y=20①}\\{12x+8y=180②}\end{array}\right.$,
②-①×8得4x=20,
解得x=5,
把x=5代入①得y=15,
所以方程组的解为$\left\{\begin{array}{l}{x=5}\\{y=15}\end{array}\right.$,
A工程队整治河道的米数为:12x=60,
B工程队整治河道的米数为:8y=120;
答:A工程队整治河道60米,B工程队整治河道120米.
点评 此题主要考查利用基本数量关系:A工程队用的时间+B工程队用的时间=20天,A工程队整治河道的米数+B工程队整治河道的米数=180,运用不同设法列出不同的方程组解决实际问题.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 4 | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{1}{2}$ |
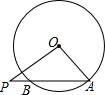 如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是$\frac{\sqrt{5}}{3}$.
如图,已知⊙O的半径为6cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA的值是$\frac{\sqrt{5}}{3}$.