题目内容
若a=2003,b=2004,c=2005,求a2+b2+c2-ab-bc-ac的值.
考点:因式分解-运用公式法
专题:计算题
分析:根据a,b,c的值求出a-b,a-c,b-c的值,原式乘以2变形后,利用完全平方公式化简,将各自的值代入计算即可求出值.
解答:解:∵a=2003,b=2004,c=2005,
∴a-b=-1,a-c=-2,b-c=-1,
则原式=
×2(a2+b2+c2-ab-bc-ac)=
[(a-b)2+(a-c)2+(b-c)2]=3.
∴a-b=-1,a-c=-2,b-c=-1,
则原式=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了因式分解-运用公式法,熟练掌握公式是解本题的关键.

练习册系列答案
相关题目
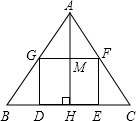 如图,已知△ABC,矩形GDEF的DE边在BC边上,G,F分别在AB,AC边上,BC=5cm,S△ABC=30cm2,AB为△ABC在BC边上的高,求△ABC的内接长方形GDEF的最大面积.
如图,已知△ABC,矩形GDEF的DE边在BC边上,G,F分别在AB,AC边上,BC=5cm,S△ABC=30cm2,AB为△ABC在BC边上的高,求△ABC的内接长方形GDEF的最大面积.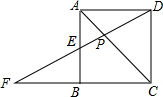 如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长.
如图,正方形ABCD中,F是CB延长线上的一点,DF交AB于E,交对角线AC于P,如PE=2,EF=3.求PD的长. 如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE=
如图,在等腰三角形ABC中,∠BAC=120°,D为BC的中点,DE⊥AB于E,求证:AE= 如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是
如图,在边长为2的正△ABC中,点E为线段BC的中点,点P为线段AC上的动点,在BP绕点B顺时针方向旋转过程中,点P的对应点为P1,设EP1=t,则t的范围是