题目内容
如图，在边长为2的正△ABC中，点E为线段BC的中点，点P为线段AC上的动点，在BP绕点B顺时针方向旋转过程中，点P的对应点为P1，设EP1=t，则t的范围是考点：旋转的性质
专题：
分析：根据正三角形的性质得出AE的长，进而利用旋转的性质以及勾股定理得出EP1的最值即可．
解答：解：∵在边长为2的正△ABC中，点E为线段BC的中点，
∴AE⊥BC，
∴AE=
=
，
由题意可得出：
当P点在A点时，旋转过程中对应点P1到E点距离最大为AE长度为
，
当P点在AC的中点上，BP最小为
，
当BP旋转到与BC重合时，EP1最小等于：BP-BE=
-1，
∴设EP1=t，则t的范围是：
-1≤t≤
．
故答案为：
-1≤t≤
．
∴AE⊥BC，
∴AE=
| 22-12 |
| 3 |
由题意可得出：
当P点在A点时，旋转过程中对应点P1到E点距离最大为AE长度为
| 3 |
当P点在AC的中点上，BP最小为
| 3 |
当BP旋转到与BC重合时，EP1最小等于：BP-BE=
| 3 |
∴设EP1=t，则t的范围是：
| 3 |
| 3 |
故答案为：
| 3 |
| 3 |
点评：此题主要考查了正三角形的性质以及勾股定理，利用极值法得出EP1的值是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
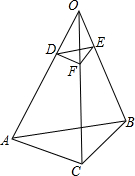如图所示，如果D、E、F分别在OA、OB、OC上，且DF∥AC，EF∥BC．求证：
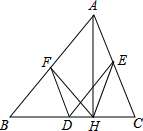如图，在△ABC中，D，E，F分别为BC，AC，AB的中点．若AH⊥BC于点H，∠BAC=60°，则∠FDE=
如图，四边形ABCD∽四边形A′B′C′D′，则CD=
数a在数轴上的位置如图所示，则
AD是△ABC的角平分线，如图，那么∠BAC=