题目内容
15.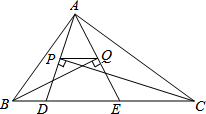 如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )| A. | 8 | B. | 6 | C. | 3 | D. | 4 |
分析 首先判断△BAE、△CAD是等腰三角形,从而得出BA=BE,CA=CD,由△ABC的周长为28,及BC=10,可得DE=8,利用中位线定理可求出PQ.
解答 解:∵△ABC的周长是26,BC=10,
∴AB+AC=28-10=18,
∵∠ABC的平分线垂直于AE,
∴在△ABQ和△EBQ中,
$\left\{\begin{array}{l}{∠ABQ=∠EBQ}\\{BQ=BQ}\\{∠AQB=∠EQB}\end{array}\right.$,
∴△ABQ≌△EBQ,
∴AQ=EQ,AB=BE,
同理,AP=DP,AC=CD,
∴DE=BE+CD-BC=AB+AC-BC=18-10=8,
∵AQ=DP,AP=DP,
∴PQ是△ADE的中位线,
∴PQ=$\frac{1}{2}$DE=4.
故选D.
点评 本题考查了三角形的中位线定理,解答本题的关键是判断出△BAE、△CAD是等腰三角形,利用等腰三角形的性质确定PQ是△ADE的中位线.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
3.-$\frac{1}{3}$的倒数是( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
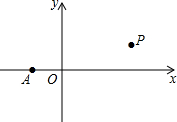 如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.
如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.