题目内容
4.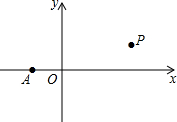 如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.
如图,在平面直角坐标系第一象限有一点P,其横坐标为3,在x轴上有一点A(-1,0),已知PA两点间的距离为2$\sqrt{5}$,则P的纵坐标为2.
分析 设P点的纵坐标为y,则P(3,y),PA=$\sqrt{(3+1)^{2}+{y}^{2}}$,又PA两点间的距离为2$\sqrt{5}$,依此为等量关系列出方程求出y的值,即可求出点P的坐标.
解答 解:设P点的纵坐标为y(y>0),则P(3,y),
依题意得$\sqrt{(3+1)^{2}+{y}^{2}}$=2$\sqrt{5}$,
解得y=±2(舍去负值).
故答案为:2.
点评 本题主要考查一元二次方程的应用,关键在于利用两点间的距离公式,用y表示出PA的值,找出等量关系,列出方程求解.平面直角坐标系中的两点间的距离公式:如果A点的坐标为(x1,y1)、B点的坐标为(x2,y2),那么AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
16.在下列各式中,不成立的是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{-2}$ | C. | -$\sqrt{{(-2)}^{2}}$ | D. | $\sqrt{-(-2)}$ |
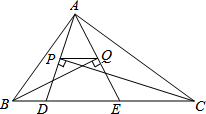 如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )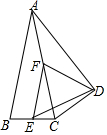 如图,在△ABC中,AB=AC=10,E、F分别是边BC、边AC的中点,以AC为斜边作Rt△ADC,DE=6,则△DEF的面积为12.
如图,在△ABC中,AB=AC=10,E、F分别是边BC、边AC的中点,以AC为斜边作Rt△ADC,DE=6,则△DEF的面积为12.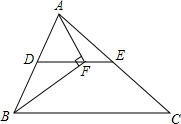 如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3.
如图,在△ABC中,BF平分∠ABC,AF⊥BF于点F,D为AB的中点,连接DF延长交AC于点E.若AB=10,BC=16,则线段EF的长为3.