题目内容
2.同一平面内的点P和图形G,给出如下定义:在图形G上若存在两点M,N,使△PMN为等边三角形,则称点P为图形G的特征点,图形G为点P的特征线,△PMN为图形G关于点P的特征三角形.(1)如图1,⊙O的半径为1,OA=$\sqrt{3}$,OB=3.在A,B两点中,⊙O的特征点是A.
若点C是⊙O的特征点,求OC长度的取值范围.
(2)如图2,在Rt△ABC中,∠C=90°,AC=1,BC=m.线段AB是点C的特征线,线段AB关于点C的特征三角形的面积为$\frac{\sqrt{3}}{9}$,求m的值.
(3)如图3,直角坐标系中的点A(-2,0),B(0,2$\sqrt{3}$),点C,D分别是射线AB和x轴上的动点,以CD为边作正方形CDEF,若△ACD是正方形CDEF关于点A的特征三角形.当正方形CDEF的一个顶点落在y轴上时,求此时正方形的边长.
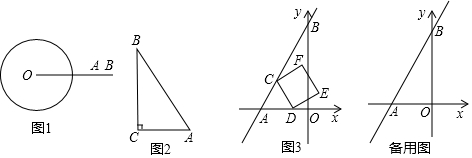
分析 (1)①根据特征点的定义即可判断;②如图2中,当CE、CF是⊙O切线,△CEF是等边三角形时,OC的值最大,最大值为2.由此即可解决问题;
(2)如图3中,作CD⊥AB于点D.由线段AB是点C的特征线,推出CD为线段AB关于点C的特征三角形的高.由线段AB关于点C的特征三角形的面积为$\frac{\sqrt{3}}{9}$,推出CD=$\frac{\sqrt{3}}{3}$,由此即可解决问题;
(3)分四种情形画出图形一一解决即可;
解答 解:(1)如图1中,观察图象可知,⊙O的特征点是点A.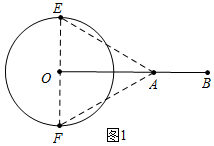
故答案为A;
如图2中,当CE、CF是⊙O切线,△CEF是等边三角形时,OC的值最大,最大值为2.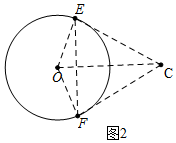
观察图象可知,0≤OC≤2.
(2)如图3中,作CD⊥AB于点D.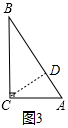
∵线段AB是点C的特征线,
∴CD为线段AB关于点C的特征三角形的高.
∵线段AB关于点C的特征三角形的面积为$\frac{\sqrt{3}}{9}$,
∴CD=$\frac{\sqrt{3}}{3}$,
∵AC=1,
∴AD=$\frac{\sqrt{6}}{3}$,
∴cosA=$\frac{AD}{AC}$=$\frac{\sqrt{6}}{3}$,
∵∠ACB=∠CDA=90°,
∴∠A=∠BCD,
∴BC=$\frac{CD}{cos∠BCD}$=$\frac{\frac{\sqrt{3}}{3}}{\frac{\sqrt{6}}{3}}$=$\frac{\sqrt{2}}{2}$,
∴m=$\frac{\sqrt{2}}{2}$.
(3)①如图4中,点E落在y轴上时,设CD=x.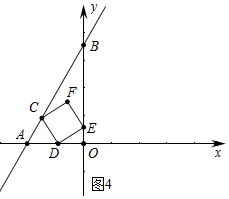
则有AD+OD=OA,
x+$\frac{\sqrt{3}}{2}$x=2,
∴x=8-4$\sqrt{3}$
∴CD=8-4$\sqrt{3}$;
②如图5中,点F落在y轴上时,设CD=x.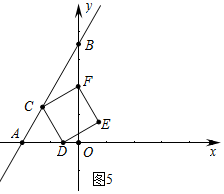
由AC+BC=AB,可得x+2•$\frac{\sqrt{3}}{2}$x=4,
∴x=2$\sqrt{3}$-2,
∴CD=2$\sqrt{3}$-2;
③如图6中,点D落在y轴上时,此时点D与点O重合,CD=2;
④如图7中,点C落在y轴上时,此时点C与点B重合,CD=4.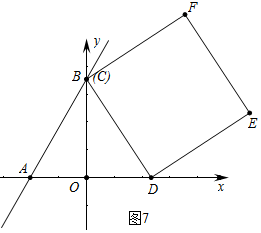
综上所述,满足条件的CD的值为8-4$\sqrt{3}$或2$\sqrt{3}$-2或2或4.
点评 本题考查圆综合题、切线的性质、等边三角形的性质.正方形的性质、锐角三角函数等知识,解题的关键是理解题意,学会用方程的思想思考问题,学会分类讨论,注意不能漏解,属于中考压轴题.

 如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )
如图,在△ABC中,点D为AB上一点,过点D作BC的平行线交AC于点E,过点E 作 AB的平行线交BC于点F,则下列说法不正确的是( )| A. | $\frac{AD}{AB}=\frac{AE}{AC}$ | B. | $\frac{DE}{FC}=\frac{AD}{BD}$ | C. | $\frac{AD}{BF}=\frac{AE}{FC}$ | D. | $\frac{BF}{BC}=\frac{AD}{AB}$ |
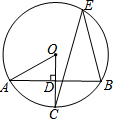 如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )
如图,A、B、E为⊙O上的点,⊙O的半径OC⊥AB于点D,已知∠CEB=30°,OD=1,则⊙O的半径为( )| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
| A. | 1.5和2之间 | B. | 1和1.5之间 | C. | 0.5和1之间 | D. | 0和0.5之间 |
| A. | 3和4之间 | B. | 4和5之间 | C. | 5和6之间 | D. | 6和7之间 |
 菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.
菱形OBCD在平面直角坐标系中的位置如图所示,顶点B(2,0),∠DOB=60°,点E坐标为(0,-$\sqrt{3}$),点P是对角线OC上一个动点,则EP+BP最短的最短距离为$\sqrt{13}$.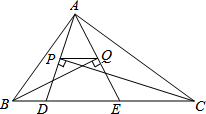 如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )