题目内容
5.两个相似多边形的最长边分别是10和30,其中一多边形的最短边为6,则另一多边形的最短边为2或18.分析 分6为最长边是10的多边形的最短边和6为最长边是30的多边形的最短边两种情况,根据相似多边形的性质列出比例式,计算即可.
解答 解:设另一多边形的最短边为x,
当6为最长边是10的多边形的最短边时,$\frac{10}{6}$=$\frac{30}{x}$,
解得,x=18,
当6为最长边是30的多边形的最短边时,$\frac{30}{6}$=$\frac{10}{x}$,
解得,x=2,
∴另一多边形的最短边为2或18,
故答案为:2或18.
点评 本题考查的是相似多边形的性质,掌握相似多边形的对应边的比相等是解题的关键.

练习册系列答案
相关题目
16.在下列各式中,不成立的是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{-2}$ | C. | -$\sqrt{{(-2)}^{2}}$ | D. | $\sqrt{-(-2)}$ |
20.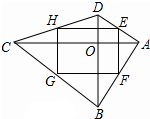 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
 在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )
在四边形ABCD中,对角线AC与BD交于点O,点E、F、G、H分别为边AD,AB,BC,CD的中点,则四边形EFGH为矩形,则需要添加的条件是( )| A. | AC平分BD | B. | AC⊥BD | C. | AC=BD | D. | AC与BD互相平分 |
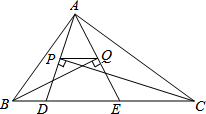 如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )
如图,△ABC的周长为28,点D,E都在边BC上,∠ABC的平分线垂直AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为( )