题目内容
4.已知x为整数,且分式$\frac{2(x+1)}{x-1}$的值为整数,则x可取的值有6个.分析 按题意分情况讨论x为整数满足分式的值为整数的取值即可,注意分母不能为0的情况.
解答 解:因为x为整数,分式$\frac{2(x+1)}{x-1}$=2+$\frac{4}{x-1}$的值也为整数,所以满足条件的有以下情况:
当x=-3时,分式值为1;
当x=-1时,分式值为0;
当x=0时,分式值为-2;
当x=1时,分式分母为0,分式无意义;
当x=2时,分式值为6;
当x=3时,分式值为4;
当x=5时,分式值为3;故满足条件的x的值为-3,-1,0,2,3,5,共6个,
故答案为:6.
点评 本题主要考查分式的性质,注意分式分母不能为0的隐性条件,此题还涉及了分类讨论思想,注意不要漏解,是解答此题的关键.

练习册系列答案
相关题目
12.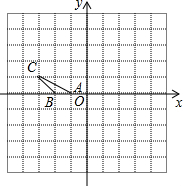 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),
B(-2,0),C(-3,1).将△ABC绕点A按顺时针方向旋转90°,得到
△AB′C′,则点B′的坐标为( )
 如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),
如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-1,0),B(-2,0),C(-3,1).将△ABC绕点A按顺时针方向旋转90°,得到
△AB′C′,则点B′的坐标为( )
| A. | (-1,1) | B. | (2,3) | C. | (4,1) | D. | (0,2) |
9.下面哪个式子的计算结果是9-x2( )
| A. | (3-x)(3+x) | B. | (x-3)(x+3) | C. | (3-x)2 | D. | (3+x)2 |
13.若$\sqrt{{{({a-1})}^2}}=1-a$,则a的取值范围是( )
| A. | a>1 | B. | a≥1 | C. | a<1 | D. | a≤1 |
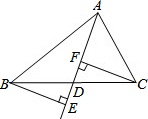 如图,BE⊥AD,CF⊥AD且BE=CF.求证:D是BC的中点.
如图,BE⊥AD,CF⊥AD且BE=CF.求证:D是BC的中点.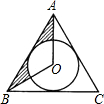 如图,已知正△ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为$\frac{27\sqrt{3}-9π}{4}$.(结果保留π)
如图,已知正△ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为$\frac{27\sqrt{3}-9π}{4}$.(结果保留π) 如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E,BC=6,△CDB的周长为15,求AC.
如图,AB=AC,AC的垂直平分线DE交AB于D,交AC于E,BC=6,△CDB的周长为15,求AC.