题目内容
15.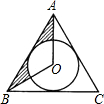 如图,已知正△ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为$\frac{27\sqrt{3}-9π}{4}$.(结果保留π)
如图,已知正△ABC的边长为9,⊙O是它的内切圆,则图中阴影部分的面积为$\frac{27\sqrt{3}-9π}{4}$.(结果保留π)
分析 要求阴影部分的面积就要明确S阴影=$\frac{1}{3}$S△ABC-$\frac{1}{3}$S⊙O,然后依面积公式计算即可.
解答 解:∵△ABC是正三角形,⊙O是它的内切圆,
∴△AOB的面积是正△ABC的$\frac{1}{3}$,扇形的面积是圆面积的$\frac{1}{3}$,
阴影部分的面积=$\frac{1}{3}$S△ABC-$\frac{1}{3}$S⊙O,
∵正△ABC的边长为9,
则正三角形的高为$\sqrt{{9}^{2}-4.{5}^{2}}$=$\frac{9\sqrt{3}}{2}$,
⊙O的半径=$\frac{3\sqrt{3}}{2}$,
∴S阴影=$\frac{1}{3}$S△ABC-$\frac{1}{3}$S⊙O=$\frac{1}{3}$($\frac{1}{2}$×9×$\frac{9\sqrt{3}}{2}$-$\frac{27}{4}$π)=$\frac{27\sqrt{3}-9π}{4}$;
故答案为:$\frac{27\sqrt{3}-9π}{4}$.
点评 本题考查了内切圆的性质、正三角形的性质、勾股定理、三角形面积公式及圆的面积公式;根据题意得出阴影部分的面积=$\frac{1}{3}$S△ABC-$\frac{1}{3}$S⊙O是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
5. 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
6.如果x2-kxy+4y2是关于x、y的完全平方式,那么k的值是( )
| A. | 2 | B. | 4 | C. | -4 | D. | 4或-4 |
20.计算(-$\frac{1}{2}$x3y)2的结果是( )
| A. | $\frac{1}{2}$x4y2 | B. | -$\frac{1}{4}$x6y2 | C. | $\frac{1}{4}$x6y2 | D. | $\frac{1}{2}$x6y2 |
7.若代数式a2-2ab=7,那么代数式3ab-$\frac{3}{2}$a2-2的值是( )
| A. | $\frac{17}{2}$ | B. | 5 | C. | -$\frac{17}{2}$ | D. | -$\frac{25}{2}$ |
5.下列计算正确的是( )
| A. | (ab3)2=a2b6 | B. | a2•a3=a6 | C. | (a+b)(a-2b)=a2-2b2 | D. | 5a-2a=3 |