题目内容
14．248-1能被60～70之间的两个整数整除，这两个整数是63，65．分析 原式利用平方差公式分解得到结果，即可作出判断．
解答 解：248-1=（224-1）（224+1）
=（212-1）（212+1）（224+1）
=（26-1）（26+1）（212+1）（224+1）
=63×65（212+1）（224+1），
则这两个整数是63，65，
故答案为：63，65
点评 此题考查了因式分解-运用公式法，熟练掌握平方差公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．下列计算正确的是（ ）
| A． | （ab3）2=a2b6 | B． | a2•a3=a6 | C． | （a+b）（a-2b）=a2-2b2 | D． | 5a-2a=3 |
已知直线y=-$\frac{1}{2}$x+2分别交x、y轴于点A、B，点C为线段OA的中点，动点P从坐标原点出发，以2个单位长度/秒的速度向终点A运动，动点Q从点C出发，以$\sqrt{2}$个单位长度/秒的速度向终点B运动．过点Q作QM∥AB交x轴于点M，动点P、Q同时出发，其中一个点到达终点，另一个点也停止运动，设点P运动的时间为t秒，PM的长为y个单位长度．
9．下列各组长度的3条线段，不能构成三角形的是（ ）
| A． | 6cm、5cm、10cm | B． | 5cm、4cm、9cm | C． | 4cm、6cm、9cm | D． | 2cm、3cm、4cm |
19．
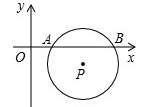如图，平面直角坐标系中，⊙P与x轴分别交于A、B两点，点P的坐标为（3，-1），AB=$2\sqrt{3}$．将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切（ ）
如图，平面直角坐标系中，⊙P与x轴分别交于A、B两点，点P的坐标为（3，-1），AB=$2\sqrt{3}$．将⊙P沿着与y轴平行的方向平移多少距离时⊙P与x轴相切（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 1或3 |
6．下列各组数不能组成直角三角形的是（ ）
| A． | a=7，b=24，c=25 | B． | a=11，b=60，c=61 | C． | a=$\frac{8}{3}$，b=2，c=$\frac{13}{3}$ | D． | a=1，b=$\frac{5}{4}$，c=$\frac{3}{4}$ |
3．若式子|x|=（x-1）0成立，则x的取值为（ ）
| A． | ±1 | B． | 1 | C． | -1 | D． | 不存在 |
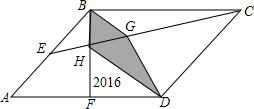如图，平行四边形ABCD中，E、F分别为AB、AD的中点，连接BF、CE交于点H，连接HD，过B点作BG平行HD，已知△HFD的面积是2016平方厘米，求阴影四边形BGDH的面积？