题目内容
14.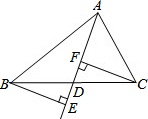 如图,BE⊥AD,CF⊥AD且BE=CF.求证:D是BC的中点.
如图,BE⊥AD,CF⊥AD且BE=CF.求证:D是BC的中点.
分析 由BE⊥AD、CF⊥AD得∠BED=∠CFD,根据BE=CF、∠BED=CFD可证△BED≌△CFD,即可得BD=CD.
解答 证明:∵BE⊥AD,CF⊥AD,
∴∠BED=∠CFD=90°,
在△BED和△CFD中,
∵$\left\{\begin{array}{l}{∠BDE=∠CDF(对顶角相等)}\\{∠BED=∠CFD}\\{BE=CF}\end{array}\right.$,
∴△BED≌△CFD(AAS),
∴BD=CD,即D是BC中点.
点评 本题主要考查全等三角形的判定和性质,将待证线段放到三角形中,证明三角形全等是证明线段相等的一种方法.

练习册系列答案
相关题目
5. 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
 按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:
按图所示程序进行计算,若首次输入x的值为-1,请把各次计算结果填入表内:| 计算次数 | 计算结果 |
| 1 | -2 |
| 2 | 4 |
| 3 | 28 |
2.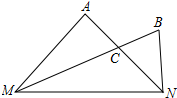 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
 如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )
如图,在MN的同侧作△AMN和△BMN,BM平分∠AMN,AN平分∠BNM,AN交BM于点C.设∠A=α°,∠B=β°,下列结论不正确的是( )| A. | 若α=β,则点C在MN的垂直平分线上 | |
| B. | 若α+β=180°,则∠AMB=∠NMB | |
| C. | ∠MCN=$(\frac{α+β}{3}+60)$° | |
| D. | 当∠MCN=120°时,延长MA、NB交于点O,则OA=OB |
9. 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )
 将右边图形绕直线旋转一周,所得的立体图形是( )
将右边图形绕直线旋转一周,所得的立体图形是( )| A. |  | B. |  | C. |  | D. |  |
6.如果x2-kxy+4y2是关于x、y的完全平方式,那么k的值是( )
| A. | 2 | B. | 4 | C. | -4 | D. | 4或-4 |
 浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?
浠水县某中学规划在校园内一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草,(如图所示),若使每一块草坪的面积都为96平方米,则人行道的宽为多少米?