题目内容
在□ABCD有任意一点O,点O到点A的距离OA=1,到点B的距离OB=2,到点C的距离OC=3,求正方形的边长.
考点:旋转的性质,勾股定理,勾股定理的逆定理,正方形的性质
专题:计算题
分析:先根据正方形的性质得BA=BC,∠ABC=90°,则可把△BOA绕点B顺时针旋转90°得到△BPC,如图,连接OP,作CH⊥BP于H,根据旋转的性质得∠OBP=90°,BP=OB=2,PC=OA=1,于是可判断△BOP为等腰直角三角形,则OP=
OB=2
,∠BPO=45°,在△OPC中利用勾股定理的逆定理得到∠OPC=90°,易得∠CPH=45°,在Rt△PCH中,根据等腰直角三角形的性质得PH=CH=
PC=
,然后在Rt△BCH中根据勾股定理计算BC.
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答:解: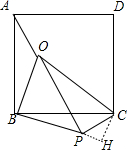 ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∴把△BOA绕点B顺时针旋转90°得到△BPC,如图,连接OP,作CH⊥BP于H,
∴∠OBP=90°,BP=OB=2,PC=OA=1,
∴△BOP为等腰直角三角形,
∴OP=
OB=2
,∠BPO=45°,
在△OPC中,∵OP=2
,OC=3,PC=1,
∴PC2+OP2=OC2,
∴△OPC为直角三角形,
∴∠OPC=90°,
∴∠BPC=∠BPO+∠OPC=135°,
∴∠CPH=180°-∠BPC=45°,
在Rt△PCH中,PH=CH=
PC=
,
∴BH=BP+PH=2+
,
在Rt△BCH中,
BC=
=
=
.
 ∵四边形ABCD为正方形,
∵四边形ABCD为正方形,∴BA=BC,∠ABC=90°,
∴把△BOA绕点B顺时针旋转90°得到△BPC,如图,连接OP,作CH⊥BP于H,
∴∠OBP=90°,BP=OB=2,PC=OA=1,
∴△BOP为等腰直角三角形,
∴OP=
| 2 |
| 2 |
在△OPC中,∵OP=2
| 2 |
∴PC2+OP2=OC2,
∴△OPC为直角三角形,
∴∠OPC=90°,
∴∠BPC=∠BPO+∠OPC=135°,
∴∠CPH=180°-∠BPC=45°,
在Rt△PCH中,PH=CH=
| ||
| 2 |
| ||
| 2 |
∴BH=BP+PH=2+
| ||
| 2 |
在Rt△BCH中,
BC=
| CH2+BH2 |
(
|
5+2
|
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质和勾股定理、勾股定理的逆定理.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
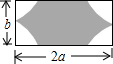 如图,在一块长为2a,宽为b的长方形铁片的四个角上截取半径都是
如图,在一块长为2a,宽为b的长方形铁片的四个角上截取半径都是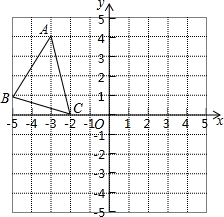 已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.
已知直角坐标系中的每个小方格的边长都是1个长度单位,△ABC的位置如图所示,现将△ABC向右平移5个单位,得到△A1B1C1,再向下平移4个单位,得到△A2B2C2.