题目内容
4.已知等腰三角形的两边长分別为a、b,且a、b满足$\sqrt{a-2}+(b-3)^{2}$=0,则此等腰三角形的周长为( )| A. | 7或8 | B. | 6或10 | C. | 6或7 | D. | 7或10 |
分析 先根据非负数的性质列式求出a、b的值,再分3是腰长与底边两种情况讨论求解.
解答 解:根据题意得,a-2=0,b-3=0,
解得a=2,b=3,
①3是腰长时,三角形的三边分别为3、3、2,
∵3+2>6,
∴能组成三角形,3+3+2=8,
②3是底边时,三角形的三边分别为3、2、2,
能组成三角形,周长=3+2+2=7,
所以,三角形的周长为7或8.
故选A.
点评 本题考查了等腰三角形的性质,绝对值非负数,偶次方非负数的性质,根据几个非负数的和等于0,则每一个算式都等于0求出a、b的值是解题的关键,难点在于要分情况讨论并且利用三角形的三边关系进行判断.

练习册系列答案
相关题目
4.在比例尺为1:4000的工地示意图上,2008年1月1日正式通车的南京地铁一号线的长度为54.3cm,那么它的实际长度( )
| A. | 0.2172km | B. | 2.172km | C. | 21.72km | D. | 217.2km |
16.$\frac{3}{4}$的倒数是( )
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | $\frac{4}{3}$ | D. | -$\frac{4}{3}$ |
14.下列图形中即是轴对称图形,又是中心对称图形的是( )
| A. | 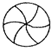 | B. |  | C. |  | D. |  |
 如图,点B在线段AD上,∠ABC=∠D,AB=ED.要使△ABC≌△EDB,则需要再添加的一个条件是BC=DB(只需填一个条件即可).
如图,点B在线段AD上,∠ABC=∠D,AB=ED.要使△ABC≌△EDB,则需要再添加的一个条件是BC=DB(只需填一个条件即可).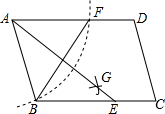 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为16.
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=12,AB=10,则AE的长为16.