题目内容
12.解方程(1)(2x+1)2=-3(2x+1)
(2)2x2-4x-9=0(用配方法解)
分析 (1)移项后分解因式,即可得出两个一元一次方程,求出方程的解即可;
(2)移项,系数化成1,配方,开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)(2x+1)2=-3(2x+1),
(2x+1)2+3(2x+1)=0,
(2x+1)(2x+1+3)=0,
2x+1=0,2x+1+3=0,
x1=-$\frac{1}{2}$,x2=-2;
(2)2x2-4x-9=0,
2x2-4x=9,
x2-2x=$\frac{9}{2}$,
x2-2x+1=$\frac{9}{2}$+1,
(x-1)2=$\frac{11}{2}$,
x-1=$±\sqrt{\frac{11}{2}}$,
x1=$\frac{2+\sqrt{22}}{2}$,x2=$\frac{2-\sqrt{22}}{2}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
12.下列各式正确的是( )
| A. | (-2x2)(-4x3)=8x5 | B. | (-x2)3=-x5 | C. | (-2x2)2=-2x4 | D. | x6÷x3=x2 |
10. 将一副三角板按图叠放,则△AOB与△COD的面积之比为( )
将一副三角板按图叠放,则△AOB与△COD的面积之比为( )
 将一副三角板按图叠放,则△AOB与△COD的面积之比为( )
将一副三角板按图叠放,则△AOB与△COD的面积之比为( )| A. | 1:$\sqrt{3}$ | B. | 1:3 | C. | 1:$\sqrt{2}$ | D. | 1:2 |
4.已知等腰三角形的两边长分別为a、b,且a、b满足$\sqrt{a-2}+(b-3)^{2}$=0,则此等腰三角形的周长为( )
| A. | 7或8 | B. | 6或10 | C. | 6或7 | D. | 7或10 |
1.一组数据3,-4,6,0,则这组数据的极差是( )
| A. | 10 | B. | 9 | C. | 3 | D. | 2.5 |
2.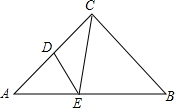 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
 如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )
如图,在Rt△ABC中,∠ACB=90°,AC=BC=6,D为AC的中点,E是线段AB边上一动点,连接ED、EC,则△CDE周长的最小值为( )| A. | 3$\sqrt{5}$ | B. | 3$\sqrt{3}$ | C. | 3$\sqrt{3}$+3 | D. | 3$\sqrt{5}$+3 |