题目内容
 如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC.
如图,已知:BE,CF为△ABC的高,P为BE上一点,BP=AC,AQ⊥AP,AQ与CF的延长线交于点Q,求证:AB=QC.考点:全等三角形的判定与性质
专题:证明题
分析:易证∠ABE=∠ACF,∠BAP=∠AQC,即可证明△ABP≌△QCA,可得AB=QC,即可解题.
解答:证明:∵∠BAC+∠ABE=90°,∠BAC+∠ACF=90°,
∴∠ABE=∠ACF,
∵∠BAP+∠QAF=90°,∠QAF+∠AQC=90°,
∴∠BAP=∠AQC,
在△ABP和△QCA中,
,
∴△ABP≌△QCA(AAS),
∴AB=QC.
∴∠ABE=∠ACF,
∵∠BAP+∠QAF=90°,∠QAF+∠AQC=90°,
∴∠BAP=∠AQC,
在△ABP和△QCA中,
|
∴△ABP≌△QCA(AAS),
∴AB=QC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ABP≌△QCA是解题的关键.

练习册系列答案
相关题目
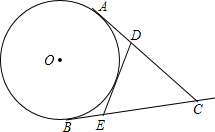 AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.
AC,BC是⊙O的两条过点C的切线,D,E分别是AC,BC边上的一点,如果△CED周长为AC的2倍,问DE与⊙O的位置关系.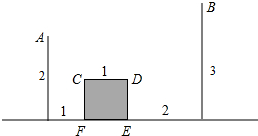 如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于
如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于 如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.
如图,在△ABD和△ACE中,∠BAD=∠CAE=90°,AD=AE,AC=AE.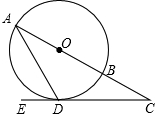 如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.
如图,在⊙O中,AB是直径,AD是弦,∠ADE=60°,∠C=30°.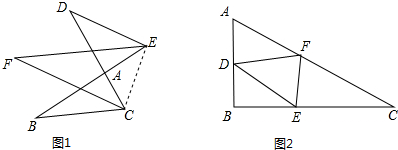
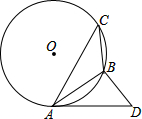 已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B,
已知AB为⊙O的弦,C为⊙O上一点,∠C=∠BAD,且BD⊥AB于点B, 小明在用图象法解二元一次方程组时所画图象如图,那么这个方程组的解是
小明在用图象法解二元一次方程组时所画图象如图,那么这个方程组的解是