题目内容
12.(1)如果a与b互为相反数,c与d互为倒数,则2(a+b)-c•d=-1(2)若(2a-1)2+|2a+b|=0,且|c-1|=2,则c•(a3-b)=$\frac{27}{8}$或-$\frac{9}{8}$
(3)已知(39+$\frac{8}{13}$)×(40+$\frac{9}{13}$)=a+b,若a是整数,1<b<2,则a=1611.
分析 (1)根据互为相反数的两个数的和为0,互为倒数的两个数的积为1求解即可.
(2)根据非负数和绝对值的性质,可求出a、b的值,然后将代数式化简再代值计算.
(3)首先把原式整理,利用整式的乘法计算,进一步根据b的取值范围得出a的数值即可.
解答 解:(1)∵a与b互为相反数,c与d互为倒数,
∴a+b=0,cd=1.
∴原式=0-1=-1.
故答案是:-1;
(2)∵(2a-1)2+|2a+b|=0
∵(2a-1)2≥0,|2a+b|≥0,
∴2a-1=0,2a+b=0,
∴a=$\frac{1}{2}$,b=-1
∵|c-1|=2,
∴c-1=±2∴c=3或-1
当a=$\frac{1}{2}$,b=-1,c=3时,c(a3-b)=3×[($\frac{1}{2}$)3-(-1)]=$\frac{27}{8}$,
当a=$\frac{1}{2}$,b=-1,c=-1时,c(a3-b)=(-1)×[($\frac{1}{2}$)3-(-1)]=-$\frac{9}{8}$.
故答案是:$\frac{27}{8}$或-$\frac{9}{8}$.
(3)解:(39+$\frac{8}{13}$)×(40+$\frac{9}{13}$)=a+b=1560+27+24$\frac{8}{13}$+$\frac{72}{169}$=1611+$\frac{176}{169}$,
∵a是整数,1<b<2,
∴a=1611.
故答案为:1611.
点评 本题考查了非负数的性质,相反数和代数式求值.一个数的偶次方和绝对值都是非负数.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
6.某小区冬季用家庭燃气炉取暖,为了估算冬季取暖第一个月使用天然气的开支情况,从11月25日起,小强连续八天每晚记录了天然气表显示的读数,如表:
小强的妈妈11月15日买了一张面值600元的天然气使用卡.已知每立方米天然气1.70元,你认为这张卡够小强家用一个月(按30天计算)吗?为什么.
| 日 期 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 | 21日 | 22日 |
| 天然气表显示的读数/m3 | 220 | 229 | 241 | 249 | 259 | 270 | 279 | 290 |
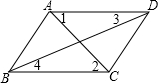 如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )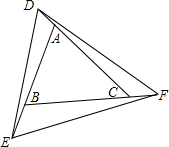 如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.
如图所示,已知△ABC,延长CA、AB、BC到D、E、F,连接DE、EF、FD,使得∠AED=∠BFE=∠CDF.若∠ABC=60°,∠DFE=50°,求∠BAC及∠EDF的度数.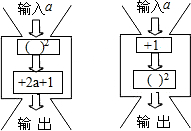 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?