题目内容
16.点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,且OA=OB,a+b≠0,则ab的值为( )| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
分析 先根据题意设出A、B两点的坐标,进而可得出结论.
解答 解:∵点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,
∴A(a,$\frac{4}{a}$),B(b,-$\frac{4}{b}$)且a>0,b<0.
∵OA=OB,a+b≠0,
∴a=-$\frac{4}{b}$,b=-$\frac{4}{a}$,
∴ab=$\frac{4}{b}$•$\frac{4}{a}$=$\frac{16}{ab}$,
∴ab=-4.
故选D.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.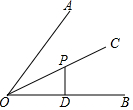 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
4.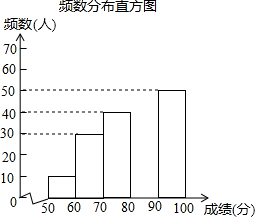 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
根据所给信息,解答下列问题:
(1)m=70,n=0.2;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表
| 成绩x(分) | 频数(人) | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
(1)m=70,n=0.2;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
11.过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
| A. | (4,$\frac{17}{6}$) | B. | (4,3) | C. | (5,$\frac{17}{6}$) | D. | (5,3) |
5.关于x的一元二次方程x2-2x+k=0有两个相等的实数根,则k的值为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
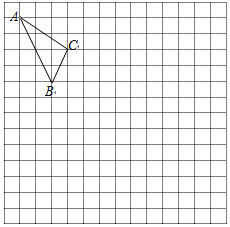 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).