题目内容
12.已知抛物线y=x2+bx-3(b是常数)经过点A(-1,0).(1)求该抛物线的解析式和顶点坐标;
(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.
①当点P'落在该抛物线上时,求m的值;
②当点P'落在第二象限内,P'A2取得最小值时,求m的值.
分析 (1)把A点坐标代入抛物线解析式可求得b的值,则可求得抛物线解析式,进一步可求得其顶点坐标;
(2)①由对称可表示出P′点的坐标,再由P和P′都在抛物线上,可得到关于m的方程,可求得m的值;②由点P′在第二象限,可求得t的取值范围,利用两点间距离公式可用t表示出P′A2,再由点P′在抛物线上,可以消去m,整理可得到关于t的二次函数,利用二次函数的性质可求得其取得最小值时t的值,则可求得m的值.
解答 解:
(1)∵抛物线y=x2+bx-3经过点A(-1,0),
∴0=1-b-3,解得b=-2,
∴抛物线解析式为y=x2-2x-3,
∵y=x2-2x-3=(x-1)2-4,
∴抛物线顶点坐标为(1,-4);
(2)①由P(m,t)在抛物线上可得t=m2-2m-3,
∵点P′与P关于原点对称,
∴P′(-m,-t),
∵点P′落在抛物线上,
∴-t=(-m)2-2(-m)-3,即t=-m2-2m+3,
∴m2-2m-3=-m2-2m+3,解得m=$\sqrt{3}$或m=-$\sqrt{3}$;
②由题意可知P′(-m,-t)在第二象限,
∴-m<0,-t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,-4),
∴-4≤t<0,
∵P在抛物线上,
∴t=m2-2m-3,
∴m2-2m=t+3,
∵A(-1,0),P′(-m,-t),
∴P′A2=(-m+1)2+(-t)2=m2-2m+1+t2=t2+t+4=(t+$\frac{1}{2}$)2+$\frac{15}{4}$;
∴当t=-$\frac{1}{2}$时,P′A2有最小值,
∴-$\frac{1}{2}$=m2-2m-3,解得m=$\frac{2-\sqrt{14}}{2}$或m=$\frac{2+\sqrt{14}}{2}$,
∵m>0,
∴m=$\frac{2-\sqrt{14}}{2}$不合题意,舍去,
∴m的值为$\frac{2+\sqrt{14}}{2}$.
点评 本题为二次函数的综合应用,涉及待定系数法、中心对称、二次函数的性质、勾股定理、方程思想等知识.在(1)中注意待定系数法的应用,在(2)①中求得P′点的坐标,得到关于m的方程是解题的关键,在(2)②中用t表示出P′A2是解题的关键.本题考查知识点较多,综合性较强,难度适中.

| A. | (2a)2=2a2 | B. | a6÷a2=a3 | C. | (a+b)2=a2+b2 | D. | a3•a2=a5 |
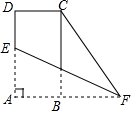 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
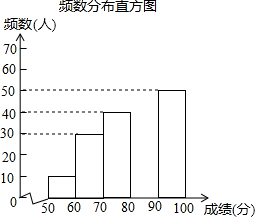 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表
| 成绩x(分) | 频数(人) | 频率 |
| 50≤x<60 | 10 | 0.05 |
| 60≤x<70 | 30 | 0.15 |
| 70≤x<80 | 40 | n |
| 80≤x<90 | m | 0.35 |
| 90≤x≤100 | 50 | 0.25 |
(1)m=70,n=0.2;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在80≤x<90分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.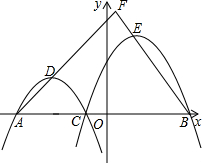 如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段A B上一点(与 A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.
如图,在平面直角坐标系xOy中,已知A,B两点的坐标分别为(-4,0),(4,0),C(m,0)是线段A B上一点(与 A,B点不重合),抛物线L1:y=ax2+b1x+c1(a<0)经过点A,C,顶点为D,抛物线L2:y=ax2+b2x+c2(a<0)经过点C,B,顶点为E,AD,BE的延长线相交于点F.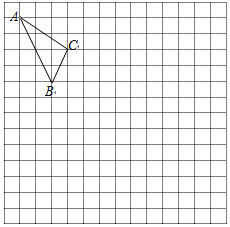 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
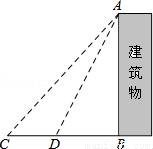
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4). 仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)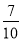 ,tan48°≈
,tan48°≈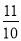 ,sin64°≈
,sin64°≈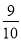 ,tan64°≈2)
,tan64°≈2)