题目内容
16.若$\frac{a}{b}$=2,$\frac{b}{c}$=6,则$\frac{a}{c}$=12.分析 由$\frac{a}{b}$=2,$\frac{b}{c}$=6得a=2b,c=$\frac{b}{6}$,代入$\frac{a}{c}$即可求得结果.
解答 解:∵$\frac{a}{b}$=2,$\frac{b}{c}$=6,
∴a=2b,c=$\frac{b}{6}$,
∴$\frac{2b}{\frac{b}{6}}$=12,
故答案为12.
点评 本题考查了有理数的除法,求得a=2b,c=$\frac{b}{6}$是解题的关键.

练习册系列答案
相关题目
4.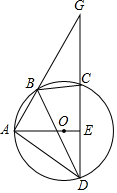 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
 如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )
如图,四边形ABCD为⊙O的内接四边形.延长AB与DC相交于点G,AO⊥CD,垂足为E,连接BD,∠GBC=50°,则∠DBC的度数为( )| A. | 50° | B. | 60° | C. | 80° | D. | 90° |
11.下列各式化简后的结果为3$\sqrt{2}$的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{36}$ |
1.以下是关于正多边形的描述:
①正多边形的每条边都相等; ②正多边形都是轴对称图形;
③正多边形的外角和是360°;④正多边形都是中心对称图形.
其中正确的描述是( )
①正多边形的每条边都相等; ②正多边形都是轴对称图形;
③正多边形的外角和是360°;④正多边形都是中心对称图形.
其中正确的描述是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①②③④ |
8.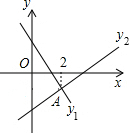 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
6.下列计算结果正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 2$\sqrt{3}$-$\sqrt{3}$=2 | C. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D. | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
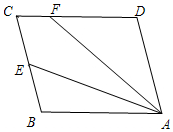 如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.
如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.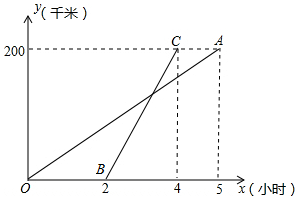 甲乙两地相距200千米,一辆货车和一辆轿车先后从甲地出发开往乙地,如图,线段OA表示货车离甲地距离y(千米)与货车行驶时间x(小时)之间的函数关系;线段BC表示轿车离甲地距离y(千米)与货车行驶时间x(小时)的函数关系,请根据图象解答下列问题:
甲乙两地相距200千米,一辆货车和一辆轿车先后从甲地出发开往乙地,如图,线段OA表示货车离甲地距离y(千米)与货车行驶时间x(小时)之间的函数关系;线段BC表示轿车离甲地距离y(千米)与货车行驶时间x(小时)的函数关系,请根据图象解答下列问题: