题目内容
18.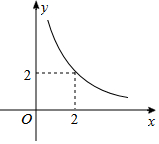 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )| A. | 4 | B. | 5 | C. | 5或3$\sqrt{2}$ | D. | 4或3$\sqrt{2}$ |
分析 根据图象得出xy=4,进而利用等腰直角三角形的性质得出x,y的值即可得出答案.
解答 解:由反比例函数的图象得xy=4,当等腰直角△ABC的斜边为底时,该底边上的高为这个底的一半,
即x=2y,2y2=4,
解得:y=$\sqrt{2}$,
则x=2$\sqrt{2}$,
∴x+y=3$\sqrt{2}$;
当等腰直角△ABC的一条直角边为底时,该底边上的高为另一条直角边,
即x=y,y2=4,
解得:y=2,
则x=2,
∴x+y=4,
综上知x+y的值为4或3$\sqrt{2}$.
故选:D.
点评 此题主要考查了反比例函数图象,正确分类讨论得出x,y的值是解题关键.

练习册系列答案
相关题目
6.在△ABC中,∠A,∠B,∠C的度数之比为2:3:4,则∠B的度数为( )
| A. | 120° | B. | 80° | C. | 60° | D. | 40° |
9. 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
 将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )
将一副三角板如图所示放置,且满足BC∥DE,则∠AFC=( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
13.已知关于x,y的二元一次方程组$\left\{\begin{array}{l}{3x+2y=a+2}\\{2x+3y=a}\end{array}\right.$的解满足x与y之和为2,求a的值.
10.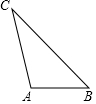 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
 如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )
如图,△ABC是一块三条边长均不相等的薄板,要在△ABC薄板中裁剪出一个面积最大的圆形薄板,则圆形薄板的圆心应是△ABC的( )| A. | 三条高的交点 | B. | 三条中线的交点 | ||
| C. | 三边垂直平分线的交点 | D. | 三个内角角平分线的交点 |
8.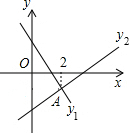 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
 如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )
如图,直线l1:y=-x+m与直线l2:y=kx+n相交于点A,点A的横坐标为2,P(x,y1)、Q(x,y2)两点分别在直线l1和直线l2上,则下列结论中错误的是( )| A. | k>0 | B. | m>n | C. | 当x<2时,y2>y1 | D. | 2k+n=m-2 |
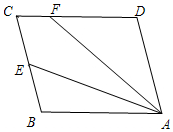 如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.
如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.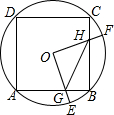 如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论:
如图,边长为2的正方形ABCD内接于⊙O,点E是$\widehat{AB}$上一点(不与A、B重合),点F是$\widehat{BC}$上一点,连接OE,OF,分别与AB,BC交于点G,H,有下列结论: