题目内容
6.已知不等式组$\left\{\begin{array}{l}{2x-a≥0}\\{3x-b<0}\end{array}\right.$的整数解为1、2、3,如果把适合这个不等式组的整数a、b组成有序数对(a,b),那么对应在平面直角坐标系上的点共有的个数为6.分析 首先解不等式组$\left\{\begin{array}{l}{2x-a≥0}\\{3x-b<0}\end{array}\right.$,不等式组的解集即可利用a,b表示,根据不等式组的整数解为1,2,3,即可确定a,b的范围,即可确定a,b的整数解,即可求解.
解答 解:$\left\{\begin{array}{l}{2x-a≥0①}\\{3x-b<0②}\end{array}\right.$,
由①得:x≥$\frac{a}{2}$,
由②得:x<$\frac{b}{3}$,
不等式组的解集为:$\frac{a}{2}$≤x<$\frac{b}{3}$,
∵整数解有1,2,3,
在数轴上画出这个不等式组解集的可能区间,如下图
根据数轴可得:0<$\frac{a}{2}$≤1,3<$\frac{b}{3}$≤4.
由0<$\frac{a}{2}$≤1,得0<a≤2,
∴a=1,2,共2个.
由3<$\frac{b}{3}$≤4,得9<b≤12,
∴b=10,11,12,共3个.
2×3=6(个).
故适合这个不等式组的整数a,b的有序数对(a,b)共有6个.
故答案为6.
点评 本题考查了一元一次不等式组的整数解,注意各个不等式的解集的公式部分就是这个不等式组的解集.但本题是要求整数解的,所以要找出在这范围内的整数.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
16.下列说法正确的是( )
| A. | 无理数都是无限不循环小数 | B. | 有理数都是有限小数 | ||
| C. | 无限小数都是无理数 | D. | 带根号的数都是无理数 |
15.16的平方根是( )
| A. | 4 | B. | 8 | C. | ±2 | D. | ±4 |
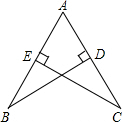 如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由.
如图,已知AB=AC,BD⊥AC,CE⊥AB,垂足分别为点D,E,说明△ABD与△ACE全等的理由. 如图?ABCD中,AC平分∠DAB,AB=5cm,AC=8cm,则?ABCD的周长为20cm,面积为24cm2.
如图?ABCD中,AC平分∠DAB,AB=5cm,AC=8cm,则?ABCD的周长为20cm,面积为24cm2.